链表是一种兼具递归和迭代性质的数据结构
技巧 1. 需要创造一条新链表的时候，可以使用虚拟头结点简化边界情况的处理。
js
var mergeTwoLists = function(l1, l2) {
// 虚拟头结点
var dummy = new ListNode(-1),
var p = dummy;
/* some codes */
p = p.next
/* some codes */
return dummy.next;
};
19. 删除链表的倒数第 N 个结点 - 力扣（LeetCode） 这道题用虚拟节点可以避免处理头节点(例如总共 2 节点，让删除倒数第 2 节点，本质是删除第一个节点，按照算法逻辑应该找到倒数第 3 个节点，但第一个节点前面已经没有节点了。)
技巧 2. 如果需要把原链表的节点接到新链表上，而不是 new 新节点来组成新链表的话，养成好习惯，把原链表的 next 连接断开。
- 一定要留意，是断开原链的 next，而不是新链的 next。
- 合一后只要能确保最后节点的 next 为 null，则不需要每次都赋值断开，因为断开的目的就是确保字不形成环，而形成环往往是最后节点形成。（中间不会形成环是因为中间节点的 next 都被重新赋值了）。
- 每条链最大值不在尾端的多合一，每次原链 p 往后走最好都断开 next，否则其中的一条链的最后节点 next 非 null，将会产生环。如果不每次节点 next 连接断开，可以选择在最后合并后的链，设置最后节点 next 为 null。
为了便于理解第一点，可以看以下两个例子，断开的是原链的 next。 21. 合并两个有序链表 - 力扣（LeetCode）
js
var mergeTwoLists = function(list1, list2) {
let dummy = new ListNode(-1)
let p = dummy
let p1 = list1
let p2 = list2
// 原链为 p1 p2
while(p1 && p2) {
// 由于两个链表是有序增大，可以保证合并后的最后节点next为 null.
// 所以可以不用断开原链的 next，当然要断开也可以
// 断开原链 p1 p2 的 next，而不是断开新链 p
if (p1.val < p2.val) {
p.next = p1
const temp = p1.next
p1.next = null
p1 = temp
// 此处断不断开无所谓，可以直接 p1 = p1.next
} else {
p.next = p2
const temp = p2.next
p2.next = null
p2 = temp
// 此处断不断开无所谓，可以直接 p2 = p2.next
}
p = p.next
}
if(p1){
p.next = p1
}
if (p2) {
p.next = p2
}
return dummy.next
};
js
var partition = function (head, x) {
let p = head
// 原链为 p
let dummy1 = new ListNode(-1)
let dummy2 = new ListNode(-1)
let p1 = dummy1
let p2 = dummy2
while (p) {
// 由于原链表不是有序，无法保证合并后的最后节点next为 null.
// 所以需要断开原链的 next，或者设置最后节点 next 为 null
// 断开原链 p 的 next，而不是断开新链 p1 p2
if (p.val < x) {
p1.next = p
p1 = p1.next
} else {
p2.next = p
p2 = p2.next
}
const next = p.next
p.next = null
p = next
// 或者 p = p.next 但必须在最后设置 p2.next = null
}
p1.next = dummy2.next
return dummy1.next
};
双指针
判断环起点
思路
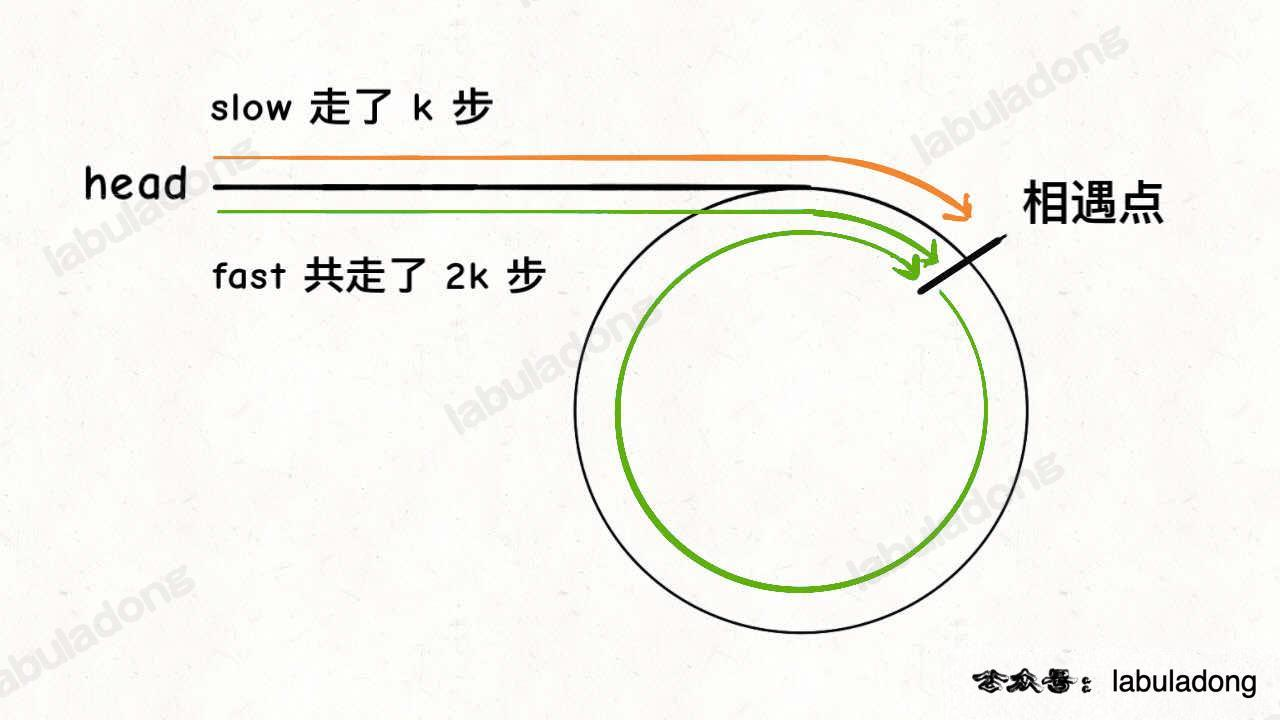
- 快慢指针，相遇时必有环。
- 相遇时，fast（2 k） 比 slow (k) 多走了 k 步，前面的 k 步是相遇点前共同走过的，后面的这 k 步是 fast 在相遇点为起点，单独在环里打圈圈，直至最后停在相遇点，所以 k 为环长度的整数倍。
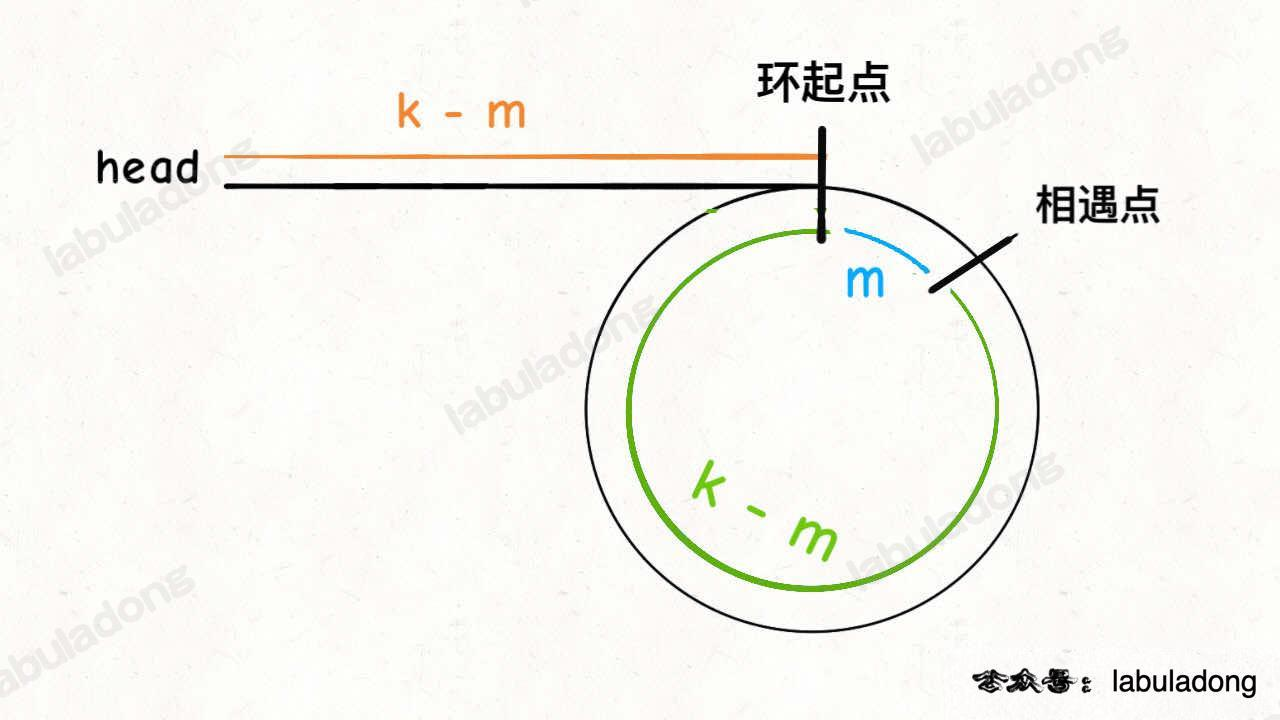
- 相遇时使得任一指针指向 head。
- 都采用 1 步进，相遇时为环起点。（图上的
k - m = k - m）。
判断两链表相交
思路 1
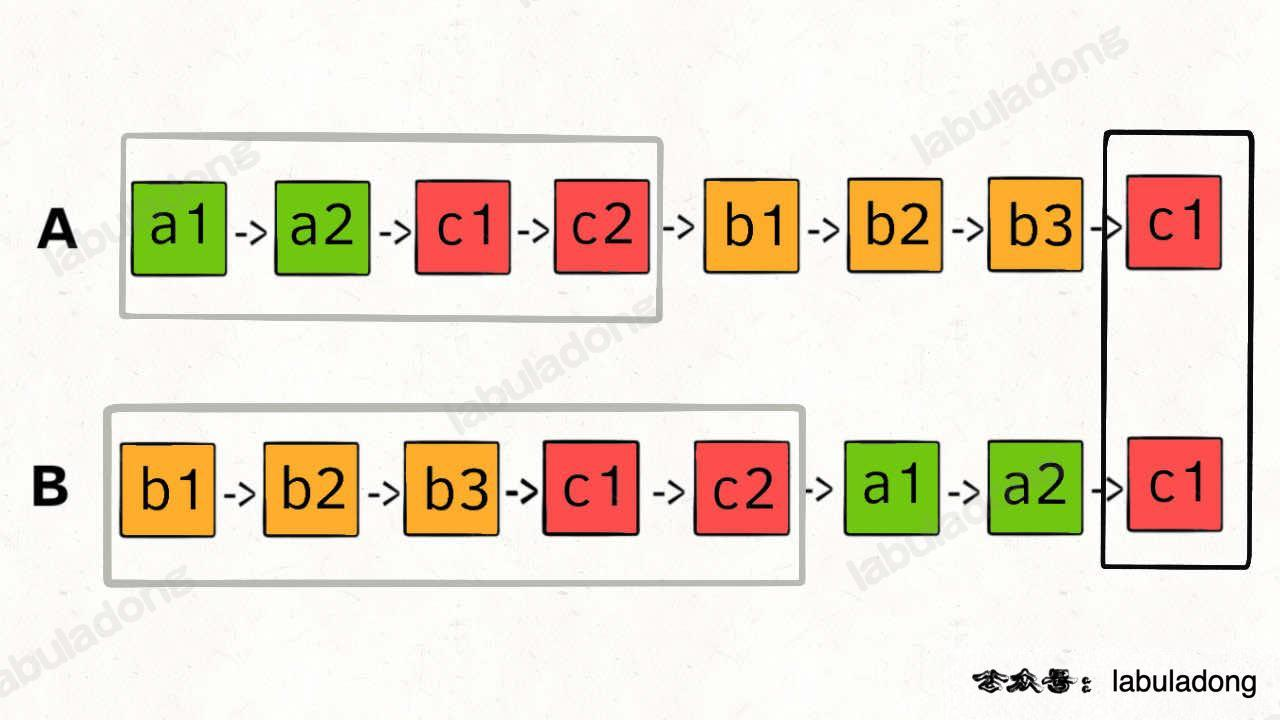
将链 A 末端接到链 B, 题目变成判断环起点，最后断开我们手动链接方便过测试。
思路 2
如果两个链有相交，则相交后都是共同部分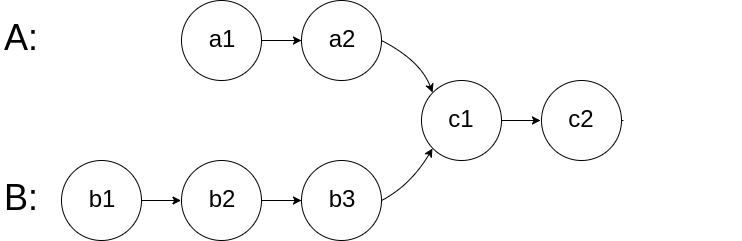 
如果在 A 链完后接着链 B，链 B 完后接着链 A，这样进行拼接，他们便拥有了彼此不同的部分
- 只要他们有相交点，保持同步进就可以同时进入公共部分，同时到达相交节点。
- 如果没有相交点，将会同时抵达 null。
反转链表
快慢指针，记录上一节点，当前节点指向上一节点即可
js
function reverse(head) {
let prev = null
let now = head
while(now) {
const next = now.next
now.next = prev
prev = now
now = next
}
return prev
}
反转链表（可以双指针，此处用递归）
简单反转
- 反转之后，尾结点变成头节点，需要返回尾节点，写出最基础框架
js
const reverseList = function(head) {
if (!head) { // 边界处理，避免 head.next 报错
return head
}
const last = reverseList(head.next)
return last // 将尾节点返回
}
- 下个节点的 next 指向自身，自身的 next 指向 null（断开链接，避免最后还要边界处理）
js
const reverseList = function(head) {
if (!head) { // 边界处理，避免 head.next 报错
return head
}
const last = reverseList(head.next)
head.next.next = head // 下个节点的 next 指向自身
head.next = null // 自身的 next 指向 null
return last // 将尾节点返回
}
- 使用到了下个节点的 next 即
head.next.next需要避免下个节点不存在。同时也意味着“如果链表为空或者只有一个节点的时候，反转结果就是它自己，直接返回即可”。
js
const reverseList = function(head) {
if (!head || !head.next) { // 边界处理，避免 head.next、head.next.next报错
return head // 如果链表为空或者只有一个节点的时候，反转结果就是它自己，直接返回即可
}
const last = reverseList(head.next)
head.next.next = head // 下个节点的 next 指向自身
head.next = null // 自身的 next 指向 null
return last // 将尾节点返回
}
这个框架是这么一步步写出来的。
反转链表前 N 个节点
还需要获取第 N+1 个节点，并将原本的头结点的 next 指向第 N+1 个节点。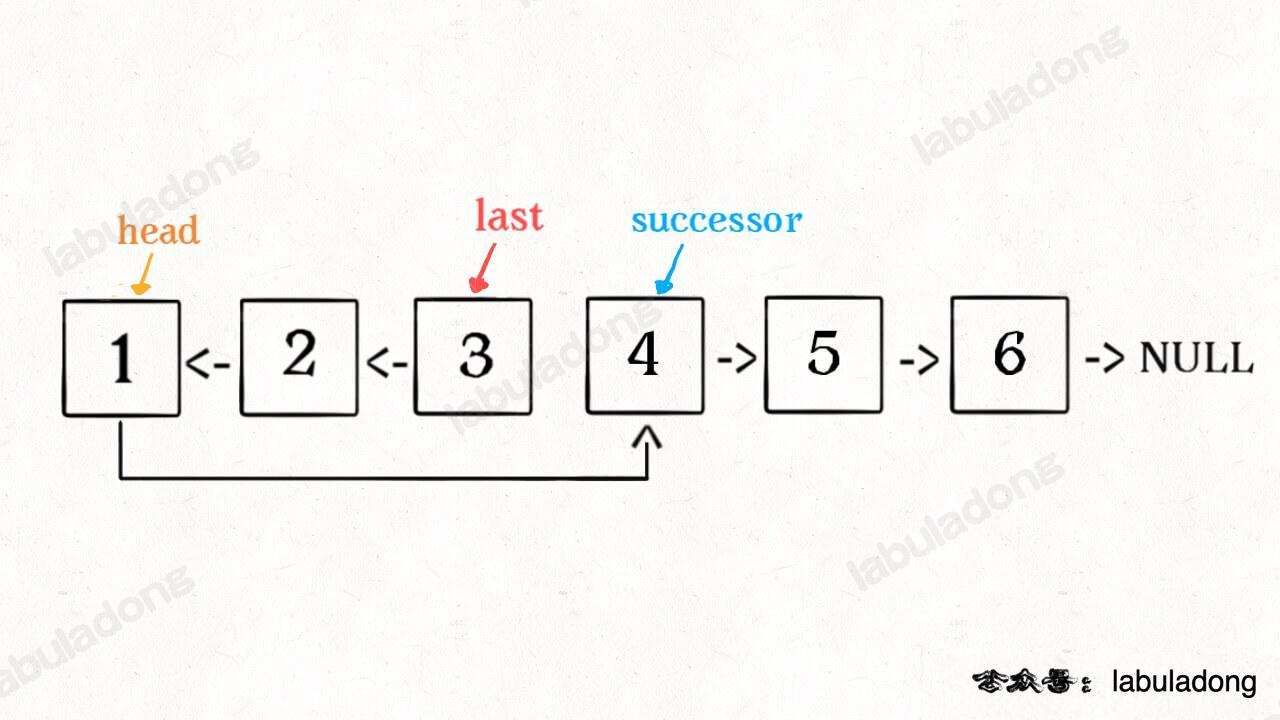 
js
let successor = null
const reverseN = function(head, n) {
// 题目n小于链表长度，所以这里可以省略
// if (!head || !head.next) { // 边界处理，避免 head.next、head.next.next报错
// return head // 如果链表为空或者只有一个节点的时候，反转结果就是它自己，直接返回即可
// }
if (n === 1) {
successor = head.next
return head //
}
const last = reverseN(head.next, n - 1)
head.next.next = head // 下个节点的 next 指向自身
head.next = successor // 自身的 next 指向 最后一个节点的next
return last // 将尾节点返回
}
反转链表的一部分
索引区间
[m, n]（索引从 1 开始），仅仅反转区间中的链表元素。
不要跳进递归，要利用明确的定义来实现算法逻辑。
- 如果
m === 1从头结点开始反转，则同《反转链表前 N 个节点》一致； - 如果
m !== 1，- 把
head的索引视为 1，那么我们是想从第m个元素开始反转； - 把
head.next的索引视为 1 ，那么相对于head.next反转的区间应该是从第m - 1个元素开始的。
- 把
js
const reverseBetween = function(head, m, n) {
// base case
if(m === 1) { // 反转以head开头的n个节点
return reverseN(head, n);
}
// 将head.next作为起点，反转前m-1个节点
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
K 个一组翻转链表
25. K 个一组翻转链表 - 力扣（LeetCode） 链表是一种兼具递归和迭代性质的数据结构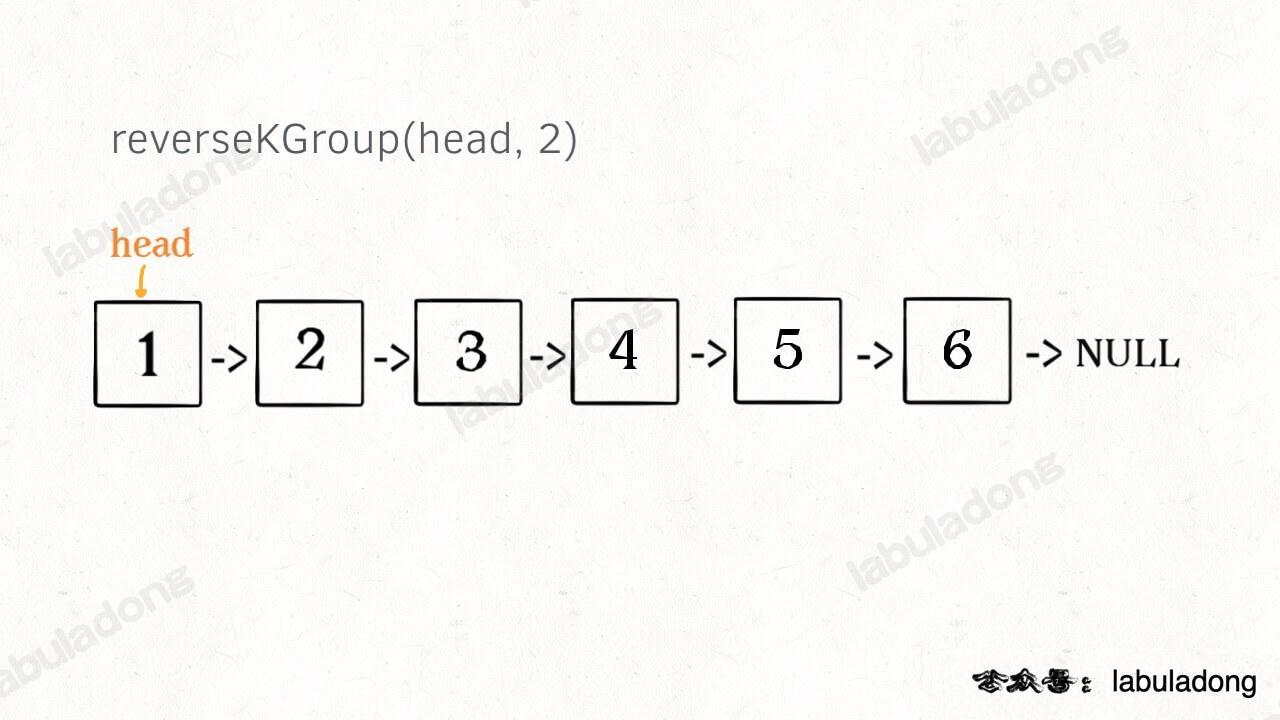 
比如对这个链表调用 reverseKGroup(head, 2)，即以 2 个节点为一组反转链表，设法把前 2 个节点反转。后面的这些节点也是一条链表，而且规模（长度）比原来这条链表小，这就叫子问题。
可以把原先的 head 指针移动到后面这一段链表的开头，因为子问题（后面这部分链表）和原问题（整条链表）的结构完全相同，这就是所谓的递归性质。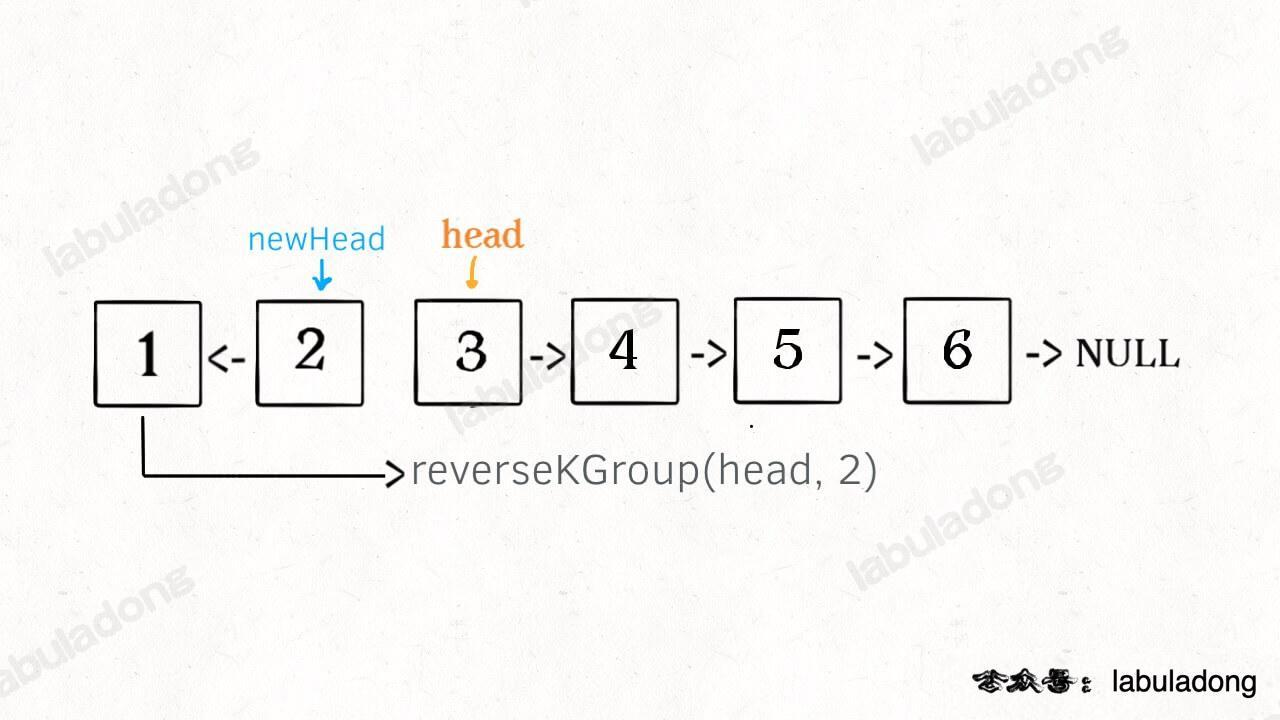 
判断回文链表
思路 1 新链表翻转再对比
思路 2 链表后续遍历
二叉树是链表的衍生，链表也有前后序。
js
var traverse = function(head) {
// 前序遍历代码
traverse(head.next);
// 后序遍历代码
}
为什么要放在后续？ 前序是进入节点时触发，进入时没什么好比较。而后序可以实现倒序打印。 在后序可以进行比较，比较后左节点转下节点。右节点本身是出栈转“下节点“
js
let left = null
var isPalindrome = function(head) {
left = head
return traverse(head)
};
const traverse = (right) => {
if (!right) return true // 到最终节点 baseCase
let res = traverse(right.next) // 子问题是否回文
// 后序遍历
// 比较，相等则true
// 比较后再转下节点
const isSame = right.val === left.val
res = res && isSame
left = left.next
return res
}
空间复杂度 O(n)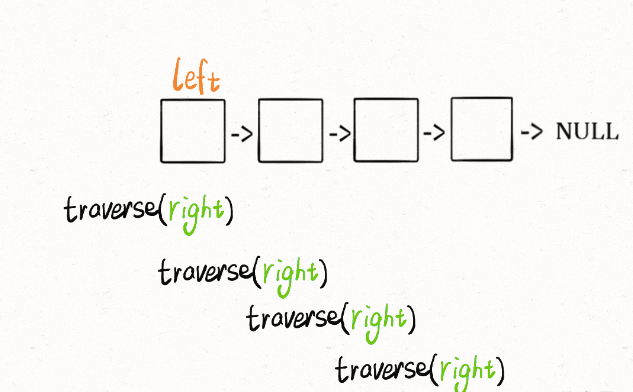
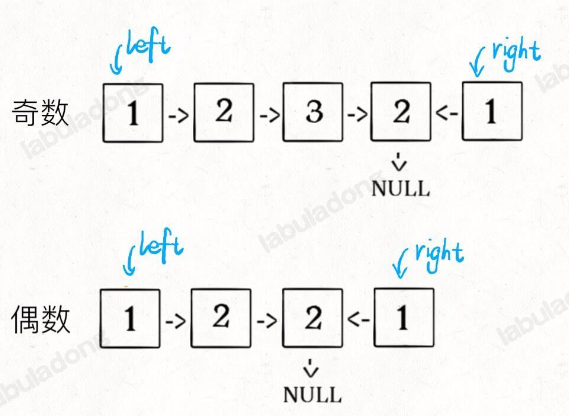
思路 3 找到中点，后半部分翻转，左右指针对比
js
var isPalindrome = function(head) {
let slow = head
let fast = head
while(fast && fast.next) {
slow = slow.next
fast = fast.next.next
}
if (fast) { // fast 有值，链为奇数链表，中点加一才是需要翻转点。
slow = slow.next //
}
let right = reverse(slow)
let left = head
while (right) { // right 为 null，证明到底了
if (right.val !== left.val) return false
right = right.next
left = left.next
}
return true
};
空间复杂度 O(1) 由于回文的特殊性，可以不完全反转链表，而是仅仅在原链表反转部分链表，将空间复杂度降到 O(1)。
优先级队列
插入或者删除元素的时候，元素会自动排序，二叉堆的操作。
上浮 swim 和下沉 sink 的操作 delMax 和 insert 基于 swim sink 实现
insert方法先把要插入的元素添加到堆底的最后，然后让其上浮到正确位置。delMax方法先把堆顶元素A和堆底最后的元素B对调，然后删除A，最后让B下沉到正确位置。
插入和删除元素的时间复杂度为 O(logK)，K 为当前二叉堆（优先级队列）中的元素总数。时间复杂度主要花费在 sink 或者 swim 上，而不管上浮还是下沉，最多也就树（堆）的高度， log 级别。
js
class PriorityQueue {
constructor() {
this.queue = [null]
this.size = 0
}
isEmpty() {
return !this.size
}
parent(x) {
return Math.floor(x/2)
}
left(x) {
return x * 2
}
right(x) {
return x * 2 + 1
}
add(val) {
this.size++
this.queue[this.size] = val
this.swim(this.size)
}
remove() {
const temp = this.queue[1]
this.swap(1, this.size)
this.queue[this.size] = null
this.size--
this.sink(1)
return temp
}
less(a, b) {
return this.queue[a].val < this.queue[b].val
}
swap(a,b) {
const temp = this.queue[a]
this.queue[a] = this.queue[b]
this.queue[b] = temp
}
swim(x) {
const parent = this.parent(x)
if (!parent || this.less(parent, x)) return
this.swap(x, parent)
this.swim(parent)
}
sink(x) {
let min = this.left(x)
if (min > this.size) return
let right = this.right(x)
if (right <= this.size && this.less(right,min)) {
min = right
}
if (min > this.size || this.less(x, min)) return
this.swap(x, min)
this.sink(min)
}
}