解题思维
「遍历」思维
通过遍历一遍二叉树得到答案 用一个 traverse 函数配合外部变量解决。（回溯算法）
「分解问题」思维
子问题（子树）的答案推导出原问题的答案，写出递归函数的定义，并充分利用返回值。（动态规划）
思考步骤
两种思维都可以解题，但某些题型用对思维会方便很多。
一旦发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码。如果第一思路判断需要借助函数返回值，直接用「分解问题」思维解题。（因为当前节点接收并利用了子树返回的信息，这就意味着你把原问题分解成了当前节点 + 左右子树的子问题。）
判断思维步骤。
- 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题。
- 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值，用「分解问题」思维解题。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
- eg: 我们定义函数
invertTree为翻转左右树，invertTree(root.left)返回翻转后的左树，invertTree(root.right)返回翻转后的右树，最后在后序位置进行翻转操作，并返回root，代表以 root 为根的这棵二叉树已经被翻转，完成定义的闭环。
- 单独抽出一个子节点，需要做什么，在前、中、后序位置哪个时候做
两个思维解题共同点：
- 单独抽出一个二叉树节点。（这一步很重要，思想上要面向一个节点）
- 在这个二叉树需要做什么事?
- 需要在 （前/中/后序位置） 分别做什么?
重点：思维不要往下递归，脑子的空间不够递归几次的。只要面对一个二叉树节点，递归函数会在所有节点执行相同的操作。
快速排序与归并排序
快速排序-前序遍历
对 nums[low..high] 进行排序，快排思路：
- 先找一个分界点
p - 通过交换元素使得
nums[low..p-1]都小于等于nums[p]，且nums[p+1..high]都大于nums[p] - 递归地去
nums[low..p-1]和nums[p+1..high]中寻找新的分界点，整个数组就被排序了
// 重点关注前序遍历位置
const sort = (nums, low, high) => {
/****** 前序遍历位置 ******/
// 通过交换元素构建分界点 p
const p = partition(nums, low, high);
/************************/
sort(nums, low, p - 1)
sort(nums, p + 1, high)
}
构造一个分界点，然后对左右子数组分别构造分界点。 先做操作，再递归。 这跟二叉树的前序遍历一致。 先对当前二叉树节点处理，然后对左右子树分别进行递归处理。
partition 是快排分区的代码可以不看，只要记得上面的代码结构即可
// partition 是快排分区的代码，可以不看，只要记得上面的代码结构即可
function partition(nums, low, high) {
// 定义基准元素
const pivot = nums[high];
let i = low - 1;
for (let j = low; j < high; j++) {
// 如果当前元素小于基准元素
if (nums[j] < pivot) {
i++;
// 交换 arr[i] 和 arr[j]
const temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
// 交换 arr[i+1] 和 arr[high]
const pivotIndex = i + 1;
const temp = nums[pivotIndex];
nums[pivotIndex] = nums[high];
nums[high] = temp;
return pivotIndex // 返回分界点
}
归并排序
对 nums[low..high] 进行排序，归并排序思路：
- 去中点
mid， 对nums[low..mid]进行排序，再对nums[mid+1..high]排序 - 最后把这两个有序的子数组合并，整个数组就排好序了 归并排序是一个后序遍历。
// 定义：排序 nums[low..high]
// 重点关注后序遍历位置
function mergeSort(nums, low, high) {
if (low >= high) return
const mid = (low + high) / 2;
// 排序 nums[low..mid]
mergeSort(nums, low, mid);
// 排序 nums[mid+1..hi]
mergeSort(nums, mid + 1, high);
/****** 后序位置 ******/
// 此时两部分子数组已经被排好序
// 合并 nums[low..mid] 和 nums[mid+1..high]
merge(nums, low, mid, high);
/*********************/
}
先递归，再做操作。 这跟二叉树的后序遍历一致。 先对左右子树分别进行递归处理，然后对当前二叉树节点处理。
数组和链表的前/后序
/* 数组-迭代遍历 */
for(let i = 0; i < arr.length; i++) {
/* some codes */
}
/* 数组-递归遍历 */
function traverse(arr, i = 0) {
if(arr.length === i) return
/* some codes 前序位置 */
traverse(arr, ++i)
/* some codes 后序位置 */
}
/* ----------- */
/* 链表-迭代遍历 */
for(let p = head; p; p = p.next) {
/* some codes */
}
/* 链表-递归遍历 */
function traverse(head) {
if(!head) return
/* some codes 前序位置 */
traverse(head.next)
/* some codes 后序位置 */
}
可以看出
- 前序位置：刚进入节点时
- 后序位置：即将离开节点时
数组和链表都可以迭代和递归，二叉树本质是二叉链表，但不好简单实现迭代，所以见到的都是递归遍历。
前序位置如果只写了打印，那便是前序遍历（中序后序同理），只要关注当前节点，在该位置写代码，迭代遍历将会在所有节点上都执行相同操作。
二叉树前/中/后序位置的区别
时间点
前/中/后序位置，对节点而言，本质上是时间点的不同。
- 前序位置：刚进入了节点时
- 中序位置：离开左节点后，进入右节点前
- 后序位置：即将离开节点时
前序位置的代码执行是自顶向下。 后序位置的代码执行是自底向上。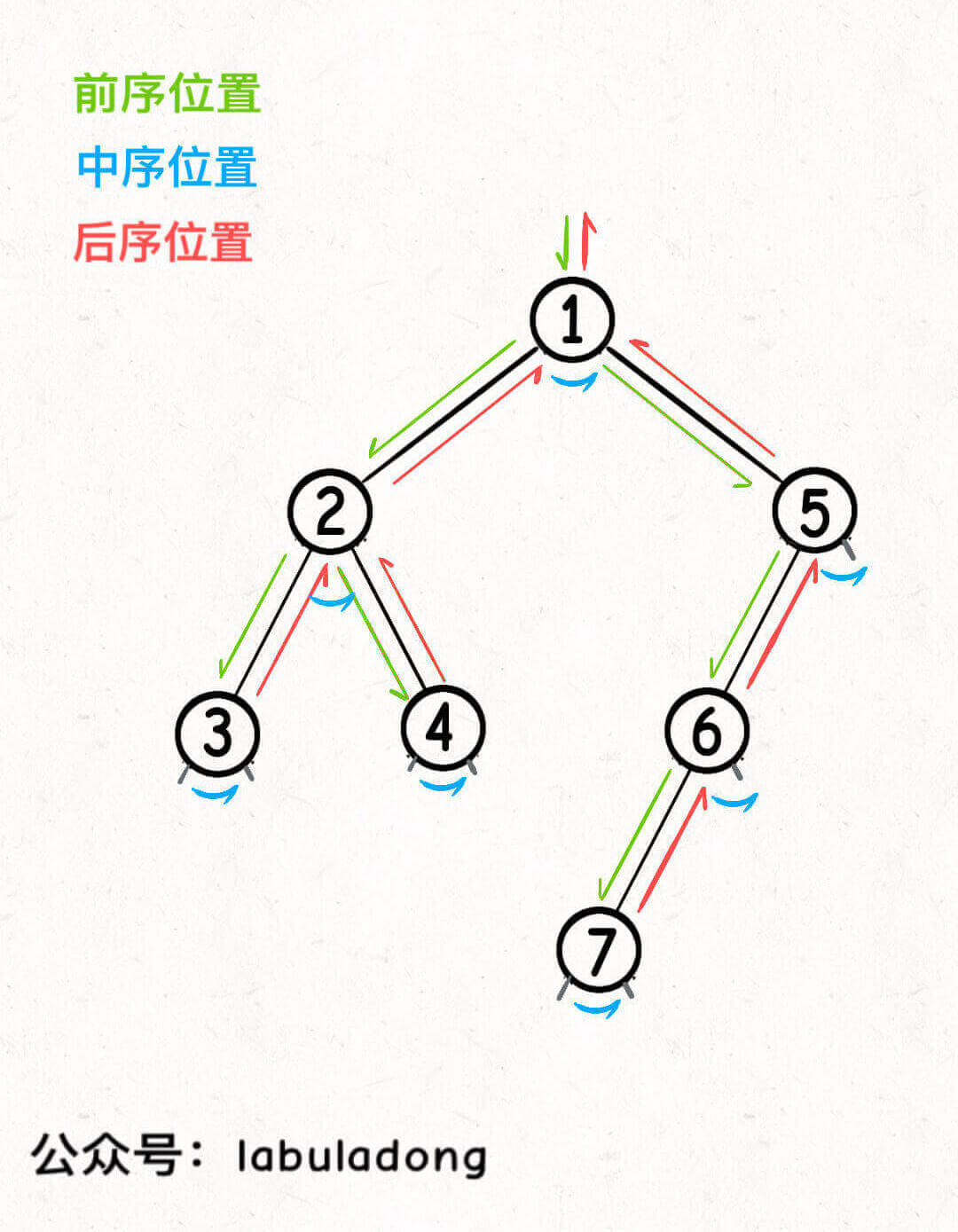 
/* 二叉树遍历 */
function traverse(root) {
if(!root) return
/* some codes 前序位置 */
traverse(root.left)
/* some codes 中序位置 */
traverse(root.right)
/* some codes 后序位置 */
}
多叉树没有「唯一」中序位置的原因，因为有太多子节点，会切换子节点树去遍历，该时间点没太大作用。
中序位置可以用于二叉搜索树，二叉搜索树在中序遍历的过程中，就是有序序列。
可获取的数据
前序位置：只能从函数参数中获取父节点传递来的参数数据，对获取数据不敏感的代码可以写在前序位置。
后序位置：不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。 换句话说，只有后续位置才能拿到所有子树返回信息。如果题目是跟子树有关，大概率要在后序位置写代码，且设置好返回值。
题目：输出一棵树的每个节点所在的层数。 此题层数是函数参数传进来的，不需要子节点数据推导，所以可以写在前序位置。
题目：输出每个节点的左右子树各有多少节点 此题子节点个数，只能通过递归遍历完才能知道子节点数据，依赖函数返回值传递回来的数据，所以只能写在后序位置。
前/中/后序位置适用题型
前序位置：对前中后序位置不敏感的代码写在前序位置。 中序位置：主要用在 BST 场景、或者二叉搜索树（有序序列）。 后序位置：主要都是「分解问题」，因为当前节点接收并利用了子树返回的信息，这就意味着你把原问题分解成了当前节点 + 左右子树的子问题。
思维「遍历」「分解问题」的运用
「遍历」
通过遍历一遍二叉树得到答案 用一个 traverse 函数配合外部变量解决。（回溯算法）
/* 注重遍历，不注重返回值。借用外部遍历， 回溯算法*/
function maxDepth(root) {
let depth = 0,
maxDepth = 0;
function traverse(root) {
if(!root) return
depth++ // 做选择
maxDepth = Math.max(maxDepth, depth)
// 前序位置
traverse(root.left)
traverse(root.right)
// 后序位置
depth-- // 撤销选择
}
traverse(root)
return maxDepth
}
回溯算法就是二叉树遍历的「遍历」思维，借助外部变量，遍历时在前序做选择，在后序撤销选择
「分解问题」
子问题（子树）的答案推导出原问题的答案，写出递归函数的定义，并充分利用返回值。（动态规划） 一棵二叉树的最大深度可以通过子树的最大深度推导出来，这就是「分解问题」。
/* 注重返回，从子问题推出原问题答案，动态规划 */
function maxDepth(root) {
if(!root) return 0
// 当前子节点作为根节点，求最大深度，为其左右节点的最大深度+1
// 由此推出原答案
// 前序位置
const left = maxDepth(root.left)
const right = maxDepth(root.right)
// 后序位置
// 计算只能在后序，即将离开该节点，左右节点迭代遍历完才有对应数据
return 1 + Math.max(left, right)
}
以树的视角看动态规划/回溯算法/DFS 算法的区别和联系
动态规划/DFS/回溯算法都可以看做二叉树问题的扩展，只是它们的关注点不同：
- 动态规划算法属于「分解问题」的思路，它的关注点在整棵「子树」。
- 回溯算法属于「遍历」的思路，它的关注点在节点间的「树枝」。
- DFS 算法属于「遍历」的思路，它的关注点在单个「节点」。
动态规划属于「分解问题」，它的关注点在整棵「子树」
请你用分解问题的思路写一个 count 函数，计算这棵二叉树共有多少个节点。
function count(root) {
if (!root) return 0;
const left = count(root.left);
const right = count(root.right);
// 后序位置，左右子树节点数加上自己就是整棵树的节点数
return left + right + 1;
}
动态规划分解问题的思路，它的着眼点永远是结构相同的整个子问题，类比到二叉树上就是「子树」。
对比斐波那契动态规划的代码，关注点在一个个子问题的返回值上。
function fib(N) {
if (N == 1 || N == 2) return 1;
return fib(N - 1) + fib(N - 2); // 关注点在一个个子问题的返回值上
}
回溯算法属于「遍历」，它的关注点在节点间的「树枝」
请你用遍历的思路写一个 traverse 函数，打印出遍历这棵二叉树的过程
function traverse(root) {
if (!root) return;
console.log("从节点 %s 进入节点 %s", root, root.left);
traverse(root.left);
console.log("从节点 %s 回到节点 %s", root.left, root);
console.log("从节点 %s 进入节点 %s", root, root.right);
traverse(root.right);
console.log("从节点 %s 回到节点 %s", root.right, root);
}
进化成多叉树，代码为
function traverse(root) {
if (!root) return;
for (const child of root.children) {
console.log("从节点 %s 进入节点 %s", root, child);
traverse(child);
console.log("从节点 %s 回到节点 %s", child, root);
}
}
回溯算法框架：
function backtrack(...) {
for (int i = 0; i < ...; i++) {
// 做选择
...
// 例如 used[i] = true
// 进入下一层决策树
backtrack(...);
// 撤销刚才做的选择
// 例如 used[i] = false
...
}
}
回溯算法遍历的思路，它的着眼点永远是在子节点之间移动的过程，类比到二叉树上就是「树枝」。
DFS 算法属于「遍历」，它的关注点在单个「节点」
请你写一个 traverse 函数，把二叉树上的每个节点的值都加一。
function traverse(root) {
if (!root) return
root.val++
traverse(root.left)
traverse(root.right)
}
DFS 算法框架
var dfs = function(root) {
if (root == null) return;
// 做选择
console.log("我已经进入节点 "+ root +" 啦");
for (var i in root.children) {
dfs(root.children[i]);
}
// 撤销选择
console.log("我将要离开节点 "+ root +" 啦");
}
DFS 算法遍历的思路，它的着眼点永远是在单一的节点上，类比到二叉树上就是处理每个「节点」
DFS 算法和回溯算法的紧密关系
DFS 算法和回溯算法非常类似，只是在细节上有所区别
「做选择」和「撤销选择」在 for 循环里面还是外面的区别
- 回溯算法在里面
- DFS 算法在外面。
// 回溯算法把「做选择」「撤销选择」的逻辑放在 for 循环里面
var backtrack = function(root) {
if (root == null) return;
for (var i in root.children) {
// 做选择
console.log("我站在节点 "+ root +" 到节点 "+ root.children[i] +" 的树枝上");
backtrack(root.children[i]);
// 撤销选择
console.log("我将要离开节点 "+ root.children[i] +" 到节点 "+ root +" 的树枝上");
}
}
// DFS 算法把「做选择」「撤销选择」的逻辑放在 for 循环外面
var dfs = function(root) {
if (root == null) return;
// 做选择
console.log("我已经进入节点 "+ root +" 啦");
for (var i in root.children) {
dfs(root.children[i]);
}
// 撤销选择
console.log("我将要离开节点 "+ root +" 啦");
}
层序遍历
前、中、后序基本都是培养递归思路的，而层序遍历属于迭代遍历。
代码模版
var levelTraverse = function(root) {
if (!root) return;
const q = [];
q.push(root);
// 从上到下遍历二叉树的每一层
while (q.length) {
const sz = q.length;
// 从左到右遍历每一层的每个节点
for (let i = 0; i < sz; i++) {
const cur = q.shift();
// 将下一层节点放入队列
cur.left && q.push(cur.left);
cur.right && q.push(cur.right);
}
// 当前这一层遍历结束
}
}
BFS 代码框架就是从二叉树的层序遍历扩展出来的，常用于求无权图的最短路径。
思维「遍历」「分解问题」题型
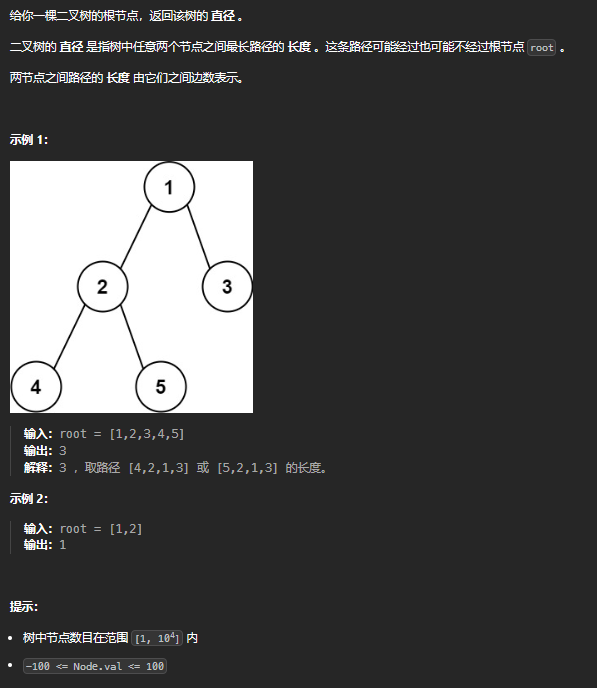
二叉树直径
最长直径，即当前节点左右子节点最大深度和。
按照思考步骤来 最大深度需要递归函数返回，如果第一思路判断需要借助函数返回值，直接用「分解问题」思维解题。
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数定义为获取当前节点树的深度，在当前函数执行递归函数，意味着子树只要执行了函数便会获取子树的深度。 要实现题目要求，当处于一个节点时，需要实现以下步骤
- 获取左子树深度，右子树深度。
- 直径为左深度+右深度，借助外部变量，记录最长直径。（操作，需要子函数返回值，写在后序位置）
- 定义返回值，左深度和右深度最大并加一，完成定义闭环。
var diameterOfBinaryTree = function(root) {
let maxLength = 0
const traverse = (root) => {
if(!root) return 0 // 当前无节点，深度为0
const left = traverse(root.left)
const right = traverse(root.right)
// 最长直径，即当前节点左右子节点最大深度和。
maxLength = Math.max(maxLength, left + right)
return Math.max(left, right) + 1 // 左右子节点最大的 + 1
}
traverse(root)
return maxLength
};
尝试 「遍历」思维 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题 暂无思路
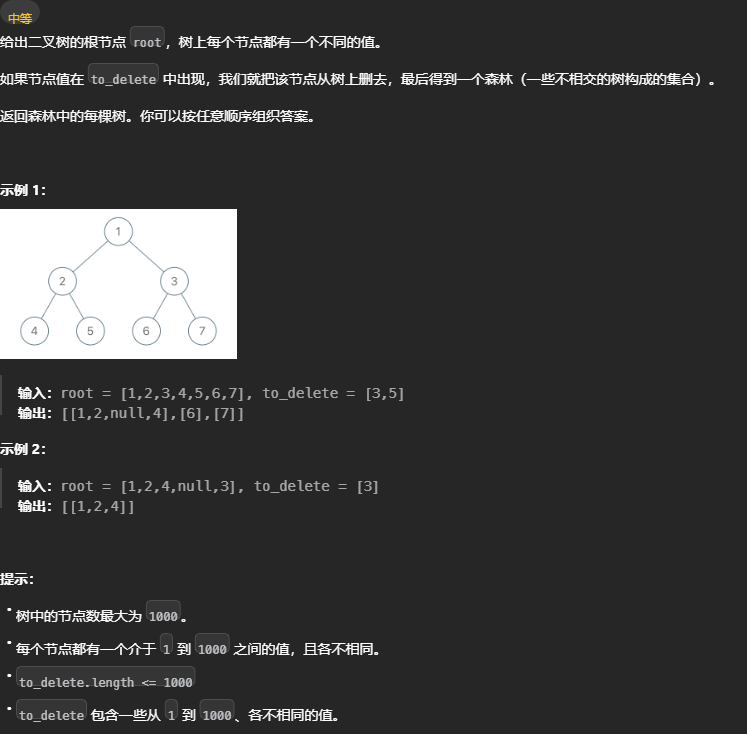
删点成林
删除自身，需要父节点来删除，所以需要利用返回值通知父节点删除。
按照思考步骤来 通知父节点删除需要递归函数返回，如果第一思路判断需要借助函数返回值，直接用「分解问题」思维解题。
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数定义为删除节点，子树函数调用后，意味着子树中也删除完成
- 自身需要被删除，如果子节点存在且没被删除，借助外部变量数组，将子节点维护到数组中。
- 子函数调用后返回
null，意味着该子节点需要被删除。子节点被删除时, 父节点赋值对应子节点null。 - 自身需要被删除，在最后返回
null，否则返回自身。(结合第 2 点可以优化，直接赋值函数调用返回值)。完成定义闭环。
function delNodes(root: TreeNode | null, to_delete: number[]): Array<TreeNode | null> {
const trees = []
const traverse = (root: TreeNode | null) => {
if (!root) return null
// 2. 子函数调用后返回 `null`，意味着该子节点需要被删除。
// 子节点被删除时, 父节点赋值对应子节点 `null`。
root.left = traverse(root.left)
root.right = traverse(root.right)
// 1. 自身需要被删除，如果子节点存在且没被删除，
// 借助外部变量数组，将子节点维护到数组中。
const needDelete: boolean = to_delete.includes(root.val)
if (needDelete) {
root.left && trees.push(root.left)
root.right && trees.push(root.right)
}
// 3. 自身需要被删除，在最后返回 `null`，否则返回自身。
// (结合第2点可以优化，直接赋值函数调用返回值)
return needDelete ? null: root
}
// 由于维护 trees 是其父节点维护的，根节点没有父节点， 特殊处理
if (root && !to_delete.includes(root.val)) {
trees.push(root)
}
traverse(root)
return trees
};
或者为了避免特殊处理，可以将 trees 维护交给子节点，告知子节点它是不是根节点。
// 1. 自身被删，告知子节点。你是根节点
// 2. 自身如果没被删，且是根节点，推入
function delNodes(root: TreeNode | null, to_delete: number[]): Array<TreeNode | null> {
const trees = []
const traverse = (root: TreeNode | null, isRoot: boolean = false) => {
if (!root) return null
const needDelete: boolean = to_delete.includes(root.val)
// 根节点，且不是删除数组内的， 推入
if (isRoot && !needDelete) {
trees.push(root)
}
// 2. 子函数调用后返回 `null`，意味着该子节点需要被删除。
// 当前节点被删除，子节点作为根节点
// 子节点被删除时, 父节点赋值对应子节点 `null`。
root.left = traverse(root.left, needDelete)
root.right = traverse(root.right, needDelete)
// 3. 自身需要被删除，在最后返回 `null`，否则返回自身。
// (结合第2点可以优化，直接赋值函数调用返回值)
return needDelete ? null: root
}
traverse(root, true)
return trees
};
尝试 「遍历」思维 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题 暂无思路
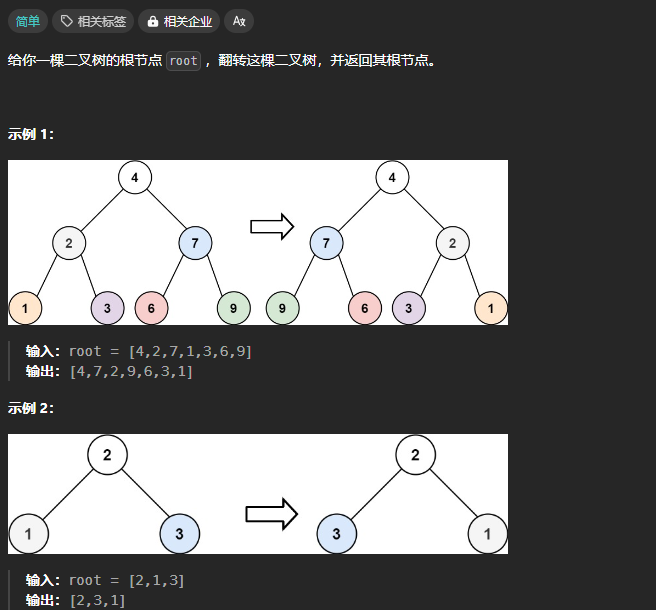
翻转二叉树
尝试 「遍历」思维 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题
通过遍历一遍二叉树得到答案，不需要依赖返回值，在前序位置操作。
// 「遍历」思维
function invertTree(root: TreeNode | null): TreeNode | null {
if (!root) return root
// 不需要依赖返回值
// 前序位置, 交换
const temp = root.left
root.left = root.right
root.right = temp
invertTree(root.left)
invertTree(root.right)
return root
};
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
我们定义函数 invertTree 为翻转左右树， invertTree(root.left) 返回翻转后的左树，invertTree(root.right) 返回翻转后的右树，最后在后序位置进行翻转操作，并返回 root，代表以 root 为根的这棵二叉树已经被翻转，完成定义的闭环。
// 「分解问题」思维
// 我们定义函数 `invertTree` 为翻转左右树
function invertTree(root: TreeNode | null): TreeNode | null {
if (!root) return root
const left = invertTree(root.left) // 返回翻转后的左树
const right = invertTree(root.right) // 返回翻转后的右树
// 需要依赖返回值
// 后序位置, 进行翻转操作
root.right = left
root.left = right
// 代表以 root 为根的这棵二叉树已经被翻转, 完成定义的闭环。
return root
};
填充节点的右侧指针
116. 填充每个节点的下一个右侧节点指针 - 力扣（LeetCode）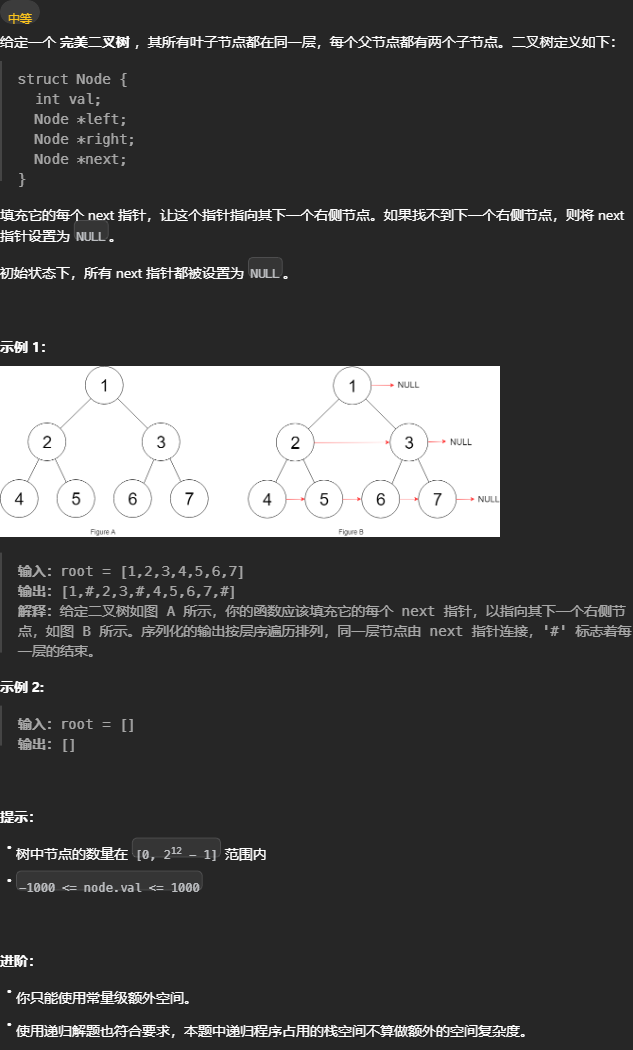
尝试 「遍历」思维 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题
通过遍历一遍二叉树得到答案，不需要依赖返回值，在前序位置操作。
由于需要连接左右两个节点，还需要连接两个相邻节点之间的「空隙」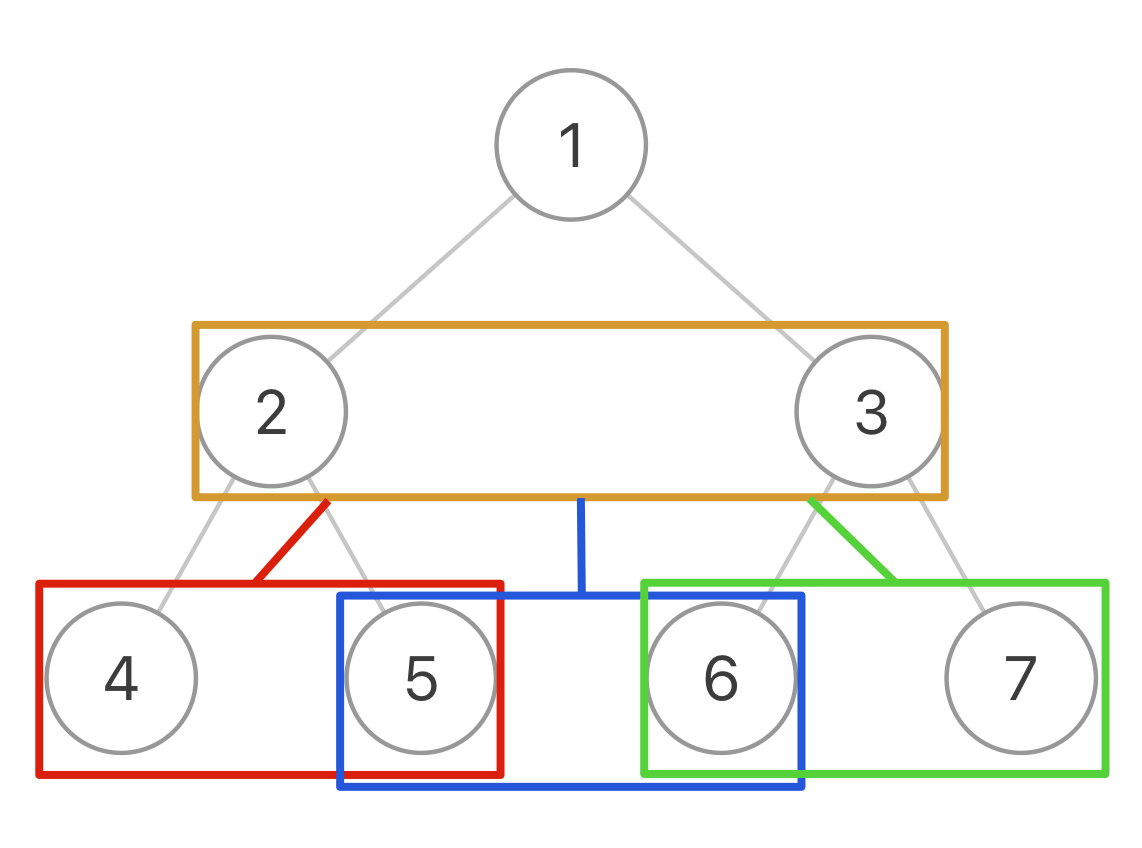
需要连接两个相邻节点的间隙，普通的遍历不满足我们，可以抛开第一个初始节点，将左右两节点作为入参，视为一个节点，这样我们就得到一颗三叉树。
在函数中执行操作，将两个节点链接起来。递归三叉树的三个节点，所有节点链接完成。
function connect(root: Node | null): Node | null {
// 可以遍历一次二叉树完成操作
// 抛开第一个初始节点，将两节点视为一个节点，这样便得到一颗三叉树
// 在函数中执行操作，将两个节点链接起来。
// 递归三叉树的三个节点，所有节点链接完成。
// 不需要依赖函数返回值, 操作可以在前序位置执行
if (!root) return null
traverse(root.left, root.right)
return root
}
function traverse(node1: Node | null, node2: Node | null): void {
if (!node1 || !node2) return
node1.next = node2
// 递归三叉树的三个节点，所有节点链接完成。
traverse(node1.left, node1.right)
traverse(node1.right, node2.left)
traverse(node2.left, node2.right)
}
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
暂无思路
本题也可以用层序遍历，不过注重的是迭代。
将二叉树展开为链表
114. 二叉树展开为链表 - 力扣（LeetCode）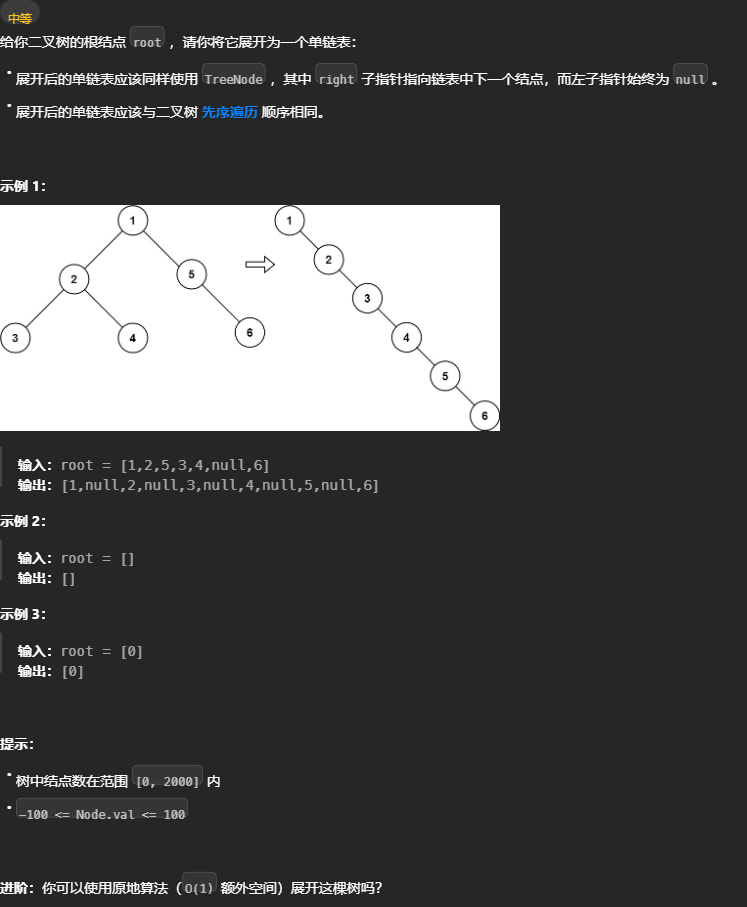
尝试 「遍历」思维 是否能通过遍历一遍二叉树得到答案，可以的话则借用外部变量，用「遍历」思维解题 不利用函数返回值，一次遍历完成，暂无思路。因为根据题目要求拉平需要左节点的最右节点，这个需要子函数返回。
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数定义为当前节点树拉平，在当前函数执行递归函数，意味着子树只要执行了函数便会被拉平 要实现题目要求，当处于一个节点时，需要实现以下步骤
- 获取左节点的最右节点(需要返回值)
- 该「最右节点的右节点」赋值为「当前节点的右节点」
- 当前左节点存在, 「当前节点的右节点」赋值为「当前节点的左节点」
- 当前节点的左节点赋值 null
- 设置返回值:
root树的最右节点为最右节点，否则为左节点最右节点，否则为本身。完成定义闭环
function flatten(root: TreeNode | null): void {
// 原函数没返回, 而我们实现功能的返回值被我们限定为「最右节点」
// 所以需要借助额外的函数 traverse
if (!root) return
traverse(root)
};
function traverse(root: TreeNode | null): TreeNode | null {
// 因为返回值被我们限定为「最右节点」
// 如果允许传入root 为 null, 那么在返回时添加需要判断
// 因为 root树 的最右节点为右节点, 否则为左节点最右节点, 否则为本身
if (!root) return null
// 1. 获取当前左节点的最右节点(需要返回值)
const leftMostRightNode = traverse(root.left)
const mostRightNode = traverse(root.right) // 取得当前最右节点
// 2. 该最右节点的右节点赋值为当前节点的右节点
if (leftMostRightNode) {
leftMostRightNode.right = root.right
}
// 3. 当前左节点存在, 当前节点的右节点赋值为当前左节点
if (root.left) {
root.right = root.left
}
// 4. 当前节点的左节点赋值null
root.left = null
// 因为 root树 的最右节点为右节点, 否则为左节点最右节点, 否则为本身
return mostRightNode || leftMostRightNode || root
}
构造二叉树
二叉树的构造问题一般都是使用「分解问题」的思路： 构造整棵树 = 根节点 + 构造左子树 + 构造右子树。
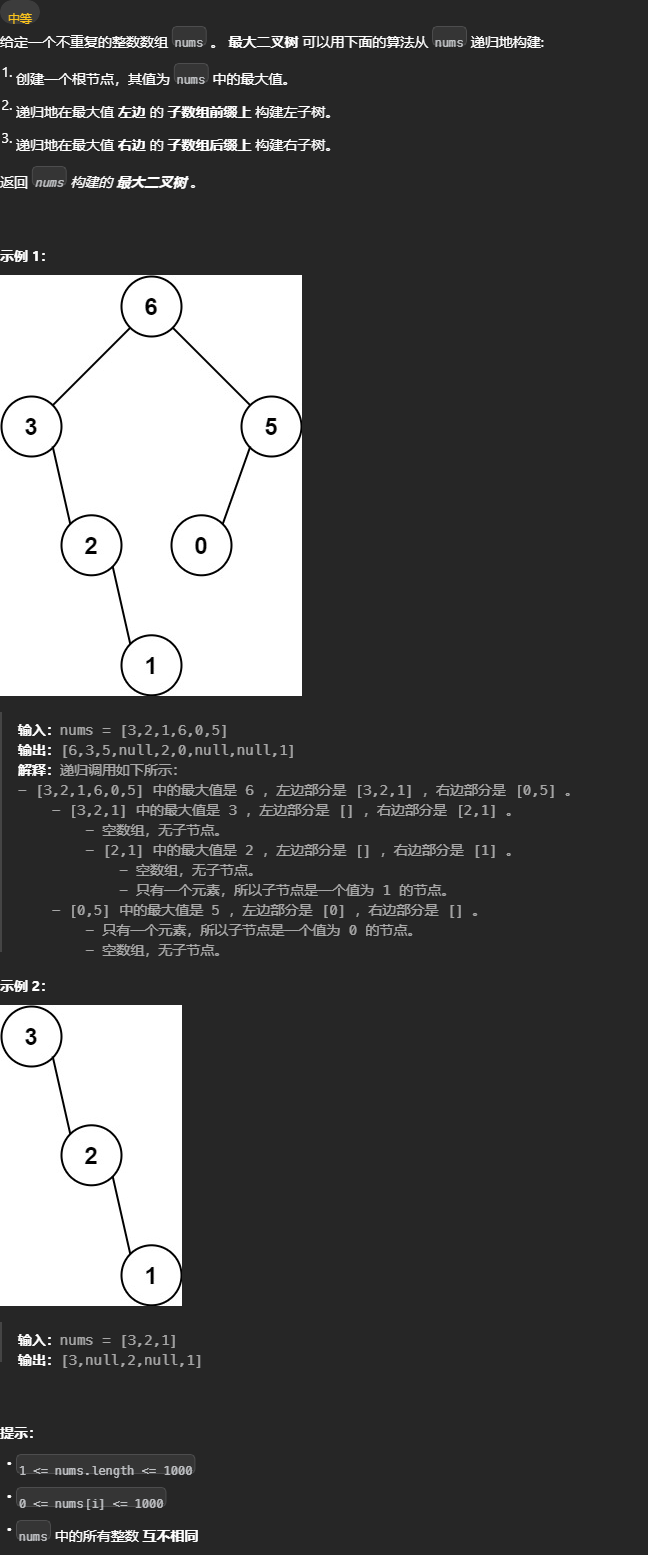
构造最大二叉树
「分解问题」的思路 函数定义为数组最大构造树，子树递归函数意味着子树也构造完最大构造树。 根节点的左右节点需要子函数构造完的树节点，所以定义函数返回为树节点
var constructMaximumBinaryTree = function(nums) {
// 创建一个根节点，其值为 nums 中的最大值。
// 递归地在最大值 左边 的 子数组前缀上 构建左子树。
// 递归地在最大值 右边 的 子数组后缀上 构建右子树。
if (!nums.length) return null
let maxIndex = -1
let max = -Infinity
for (let i = 0; i < nums.length; i++) {
if (max >= nums[i]) {
continue;
}
max = nums[i]
maxIndex = i
}
const root = new TreeNode(max);
// 当然，这里推荐用 traverse 函数，参数改为接收下标，可以避免新建数组浪费多余的空间复杂度
// 用数组的地方都可以考虑下标
root.left = constructMaximumBinaryTree(nums.slice(0, maxIndex));
root.right = constructMaximumBinaryTree(nums.slice(maxIndex + 1));
return root
};
通过前序和中序遍历结果构造二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）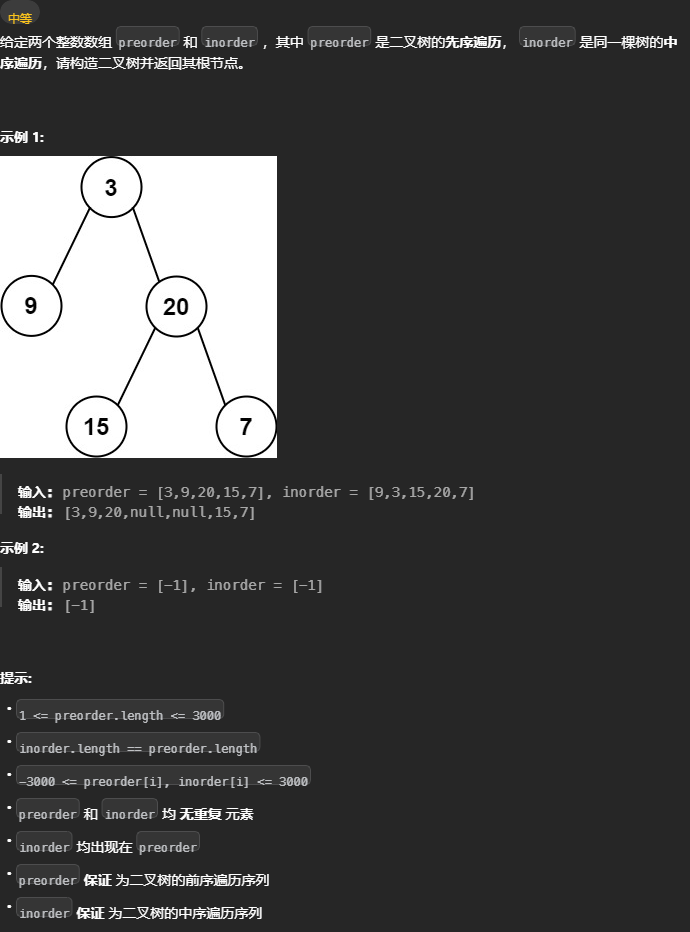
对于前序和中序打印出的数组，有以下特点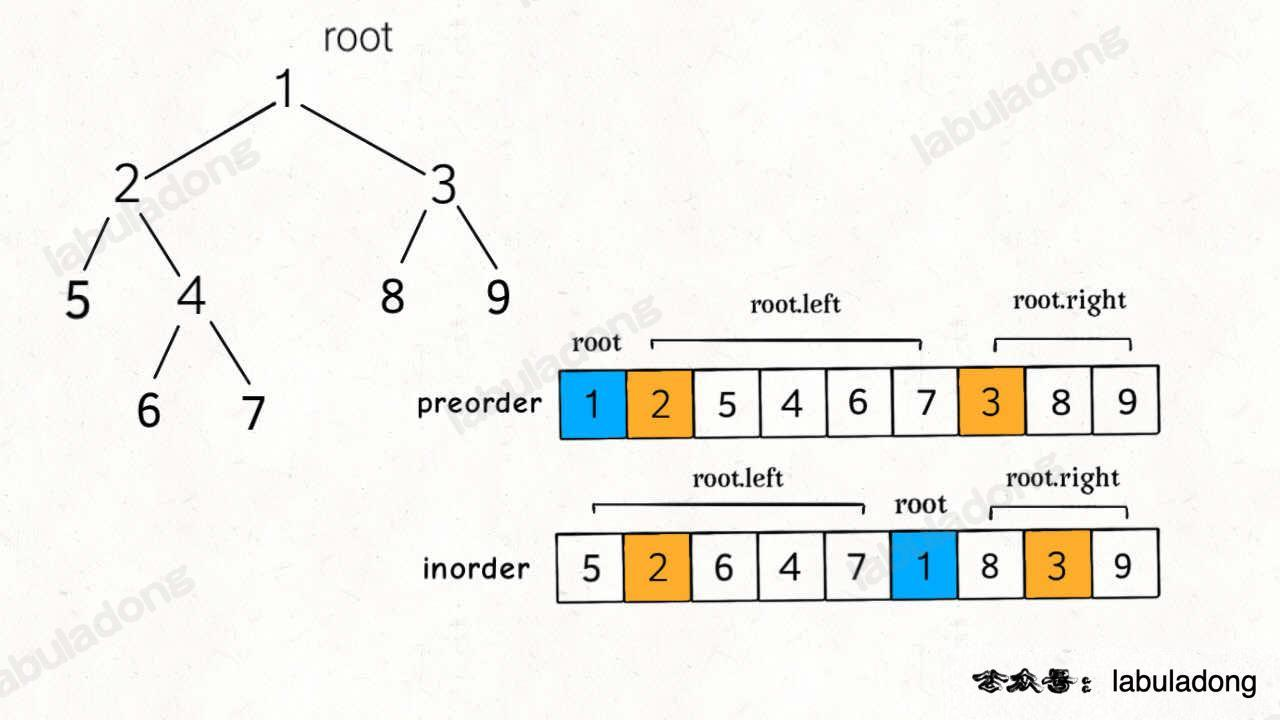 
前序数组的首位是根节点，如果要分割左右子树，需要知道左节点树的数量。 中序数组根节点前面的元素都是左节点，可以获取到左节点树的数量。
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数的定义是构建树，在当前函数执行递归函数，意味着子树也构建完成
- 用前序数组获取根节点-首位
- 在范围内中序数组查找根节点下标，下标前为左数组，后为右数组。
- 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
- 如果数组长度不为零，返回构造完的节点，否则返回
null。完成定义闭环。
var buildTree = function(preorder, inorder) {
if (preorder.length === 0) return null
// 1. 用前序数组获取根节点-首位
// 2. 在范围内中序数组查找根节点下标，下标前为左数组，后为右数组。
// 3. 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
// 4. 如果数组长度不为零，返回构造完的节点，否则返回 `null`。完成定义闭环。
const traverse = (pstart, pend, istart, iend) => {
if (pstart > pend) return null
const rootVal = preorder[pstart]
const root = new TreeNode(rootVal)
let mid = istart
while (mid <= iend && inorder[mid] !== rootVal) {
mid++
}
// 左数组长度 mid - istart
const leftLength = mid - istart
root.left = traverse(pstart + 1, pstart + leftLength, istart, mid - 1)
root.right = traverse(pstart + leftLength + 1, pend, mid + 1, iend)
return root
}
return traverse(0, preorder.length - 1, 0, inorder.length - 1)
};
通过后序和中序遍历结果构造二叉树
106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）
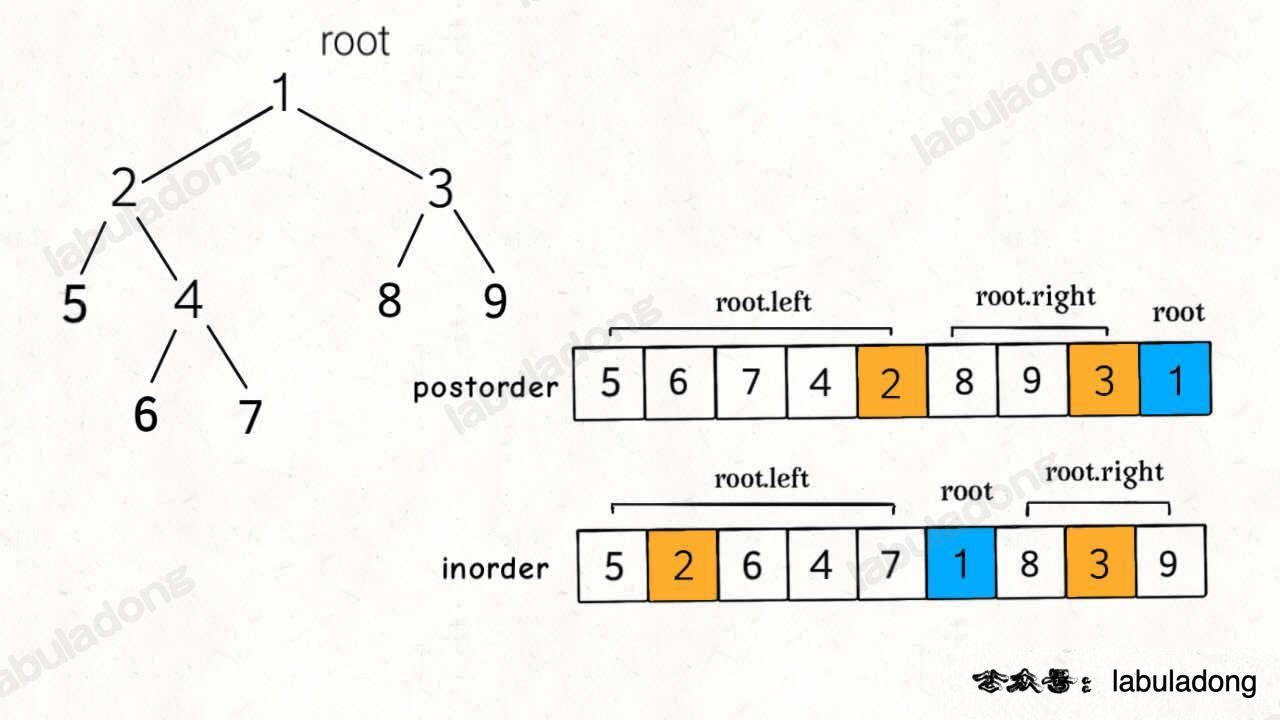
范围内 后序的根节点在最后一个 中序的根节点前都是左节点，后都是右节点
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数的定义是构建树，在当前函数执行递归函数，意味着子树也构建完成
- 用后序数组获取根节点-末位
- 在范围内中序数组查找根节点下标，下标前为左数组，后为右数组。
- 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
- 如果数组长度不为零，返回构造完的节点，否则返回
null。完成定义闭环。
var buildTree = function(inorder, postorder) {
if (postorder.length === 0) return null
// 1. 用后序数组获取根节点-末位
// 2. 在范围内中序数组查找根节点下标，下标前为左数组，后为右数组。
// 3. 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
// 4. 如果数组长度不为零，返回构造完的节点，否则返回 `null`。完成定义闭环。
const traverse = (pstart, pend, istart, iend) => {
if (pstart > pend) return null
const rootVal = postorder[pend]
const root = new TreeNode(rootVal)
let mid = istart
while (mid <= iend && inorder[mid] !== rootVal) {
mid++
}
// 左数组长度 mid - istart
const leftLength = mid - istart
root.left = traverse(pstart, pstart + leftLength - 1, istart, mid - 1)
root.right = traverse(pstart + leftLength, pend - 1, mid + 1, iend)
return root
}
return traverse(0, postorder.length - 1, 0, inorder.length - 1)
};
通过后序和前序遍历结果构造二叉树
889. 根据前序和后序遍历构造二叉树 - 力扣（LeetCode）
范围内 前序的根节点在第一位，紧接着是左值及其子树，右值及其子树 前序的根节点在第一位，第二位则是左值 和前两道题不同的是，用前序和后序构建的二叉树不唯一，但我们只要输出一种即可，如果用左值，默认左子树有
尝试 「分解问题」思维 是否能通过子问题推导得到答案，可以的话写出函数的定义，拆解子问题，利用返回值。
- 思考函数的定义是什么？
- 结合定义，在当前函数执行递归函数，意味着子树怎么了？
- 在后序位置，利用返回值执行操作，并结合操作需要去定义返回值，完成定义闭环。
函数的定义是构建树，在当前函数执行递归函数，意味着子树也构建完成
- 用前序数组获取根节点-首位，左值-第二位
- 在范围内后序数组查找左值下标，下标及其前为左数组，其后为右数组。
- 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
- 如果数组长度不为零，返回构造完的节点，否则返回
null。完成定义闭环。
var constructFromPrePost = function(preorder, postorder) {
if (preorder.length === 0) return null
// 1. 用前序数组获取根节点-首位，左值-第二位
// 2. 在范围内后序数组查找左值下标，下标及其前为左数组，其后为右数组。
// 3. 新建节点，值为根节点。左节点为左数组作为参数归函数，右节点同理。
// 4. 如果数组长度不为零，返回构造完的节点，否则返回 `null`。完成定义闭环。
const traverse = (prstart, prend, postart, poend) => {
if (prstart > prend) return null
const rootVal = preorder[prstart]
const root = new TreeNode(rootVal)
if (prstart === prend) { // 只有一长度，不需要递归子节点
return root
}
const leftVal = preorder[prstart + 1]
let left = postart
while (left <= poend && postorder[left] !== leftVal) {
left++
}
// 左数组始终间隔 left - postart
const leftLength = left - postart
root.left = traverse(prstart + 1, prstart + 1 + leftLength, postart, left)
root.right = traverse(prstart + 1 + leftLength + 1, prend, left + 1, poend - 1)
return root
}
return traverse(0, preorder.length - 1, 0, preorder.length - 1)
};
序列化
总结
序列化后结果包含空节点，且只有前序和后序，才能还原出唯一的树。
因为只有前序/后序遍历的结果中，可以确定根节点的位置，而中序遍历的结果中，根节点的位置是无法确定的。
总结，当二叉树中节点的值不存在重复时：
- 如果序列化中不包含空指针的信息，且只有一种遍历顺序，那么无法还原出唯一的一棵二叉树。
- 如果序列化中不包含空指针的信息，且有两种遍历顺序，分两种情况：
- 前序和中序，或者后序和中序，可以还原出唯一的一棵二叉树。
- 前序和后序，无法还原出唯一的一棵二叉树。(因为无法确定是左节点存在还是右节点存在)
- 如果序列化中包含空指针的信息，且只有一种遍历顺序，分两种情况：
- 前序或者后序，可以还原出唯一的一棵二叉树。
- 中序，无法还原出唯一的一棵二叉树。(因为无法确定根节点位置，而反序列**
deserialize方法首先寻找root节点的值，然后递归计算左右子节点**)
无空值表示两种遍历前后序无法唯一，有空值表示一种遍历中序无法唯一。
二叉树的序列化与反序列化
297. 二叉树的序列化与反序列化 - 力扣（LeetCode）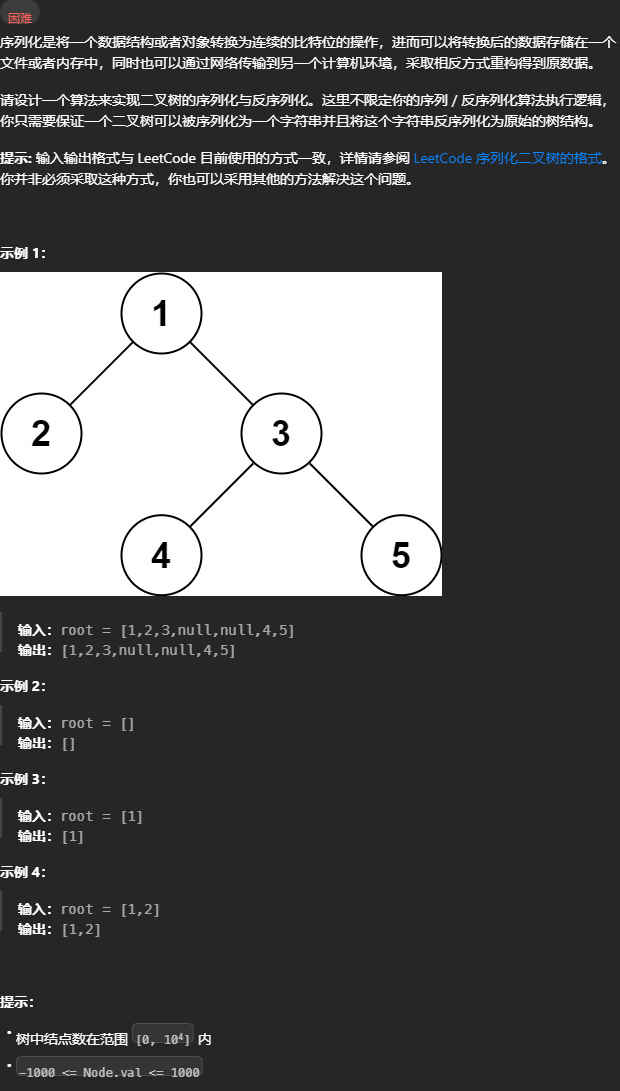
有空值表示一种遍历中序无法唯一，选前后序任意一个都行。 deserialize 方法首先寻找 root 节点的值，然后递归计算左右子节点
前序
前序数组，首位先找根节点，随后左节点，再右节点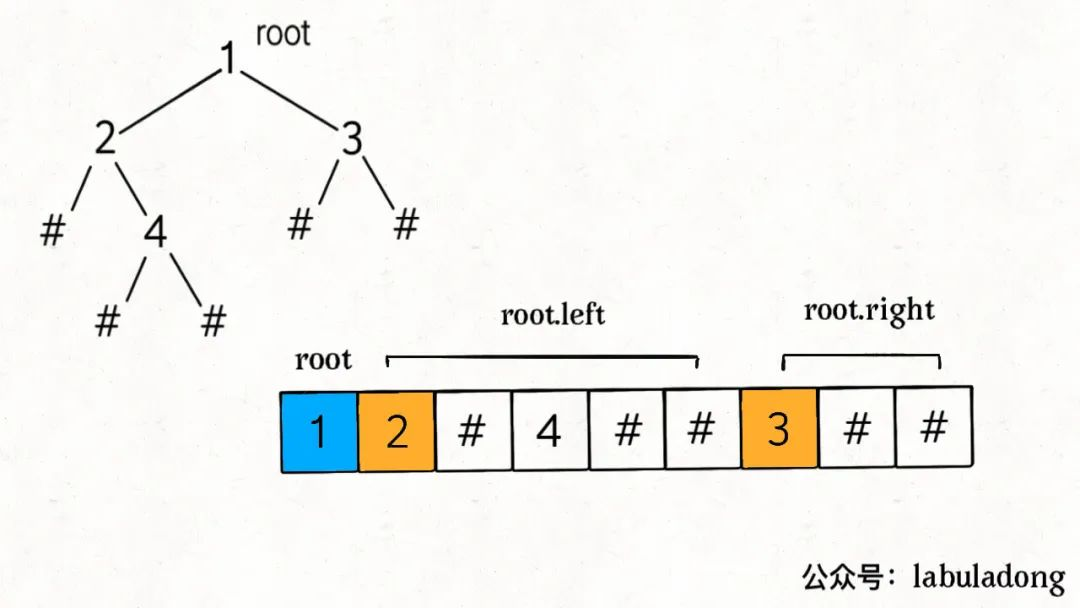 
由于前序没什么难度，此处不写解法。
后序
后序数组，先找根节点从后往前在 nodes 列表中取元素，一定要先构造 root.right 子树，后构造 root.left 子树。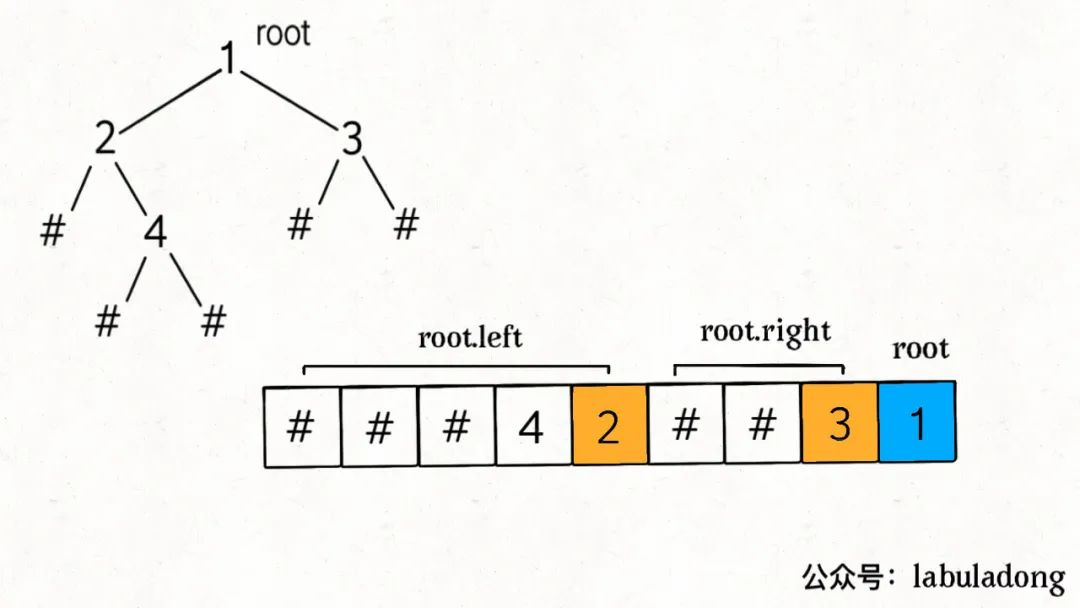 
var serialize = function(root) {
const traverse = (root) => {
if (!root) return '#'
const left = traverse(root.left)
const right = traverse(root.right)
return left + ',' + right + ',' + root.val
}
return traverse(root)
};
var deserialize = function (data) {
const arr = data.split(',')
const traverse = data => {
const str = data.pop() // 先找根节点**从后往前在 `nodes` 列表中取元素
if (str === '#') {
return null
}
const root = new TreeNode(str)
// 一定要先构造 `root.right` 子树，后构造 `root.left` 子树**。
root.right = traverse(data)
root.left = traverse(data)
return root
}
return traverse(arr)
};
层序遍历
var levelTraverse = function(root) {
if (!root) return;
const q = [];
q.push(root);
// 从上到下遍历二叉树的每一层
while (q.length) {
const sz = q.length;
// 从左到右遍历每一层的每个节点
for (let i = 0; i < sz; i++) {
const cur = q.shift();
// 将下一层节点放入队列
cur.left && q.push(cur.left);
cur.right && q.push(cur.right);
}
// 当前这一层遍历结束
}
}
上面是层序遍历模版，由于我们需要记录空节点，所以需要改造下空节点部分，空节点也推入，然后在读取的时候再判断空节点。
var serialize = function(root) {
if (!root) return '';
const ret = []
const q = [];
q.push(root);
// 从上到下遍历二叉树的每一层
while (q.length) {
const sz = q.length;
// 从左到右遍历每一层的每个节点
for (let i = 0; i < sz; i++) {
const cur = q.shift();
if (!cur) {
ret.push('#')
continue // 读取的时候再判断空节点。
}
ret.push(cur.val)
// 将下一层节点放入队列，空节点也推入
q.push(cur.left);
q.push(cur.right);
}
// 当前这一层遍历结束
}
return ret.join(',')
}
var deserialize = function(data) {
if (data === '#' || !data) return null
const q = data.split(',')
const root = new TreeNode(q.shift())
const level = [root]
// 从上到下遍历二叉树的每一层
while (q.length) {
const sz = level.length
// 从左到右遍历每一层的每个节点
for (let i = 0; i < sz; i++) {
const cur = level.shift()
const leftVal = q.shift()
const rightVal = q.shift()
cur.left = leftVal === '#'? null: new TreeNode(leftVal)
cur.right = rightVal === '#'? null: new TreeNode(rightVal)
cur.left && level.push(cur.left)
cur.right && level.push(cur.right)
}
// 当前这一层遍历结束
}
return root
};
由于此处不需要计步，不需要知道当前层有多少个点，所以可以省去 for 或 while
var deserialize = function(data) {
if (data === '#' || !data) return null
const q = data.split(',')
const root = new TreeNode(q[0])
const level = [root]
const sz = q.length
for (let i = 1; i < sz; ) { // 不用自动迭代
const cur = level.shift()
const leftVal = q[i++]
const rightVal = q[i++]
cur.left = leftVal === '#'? null: new TreeNode(leftVal)
cur.right = rightVal === '#'? null: new TreeNode(rightVal)
cur.left && level.push(cur.left)
cur.right && level.push(cur.right)
}
return root
};
寻找重复的子树
652. 寻找重复的子树 - 力扣（LeetCode）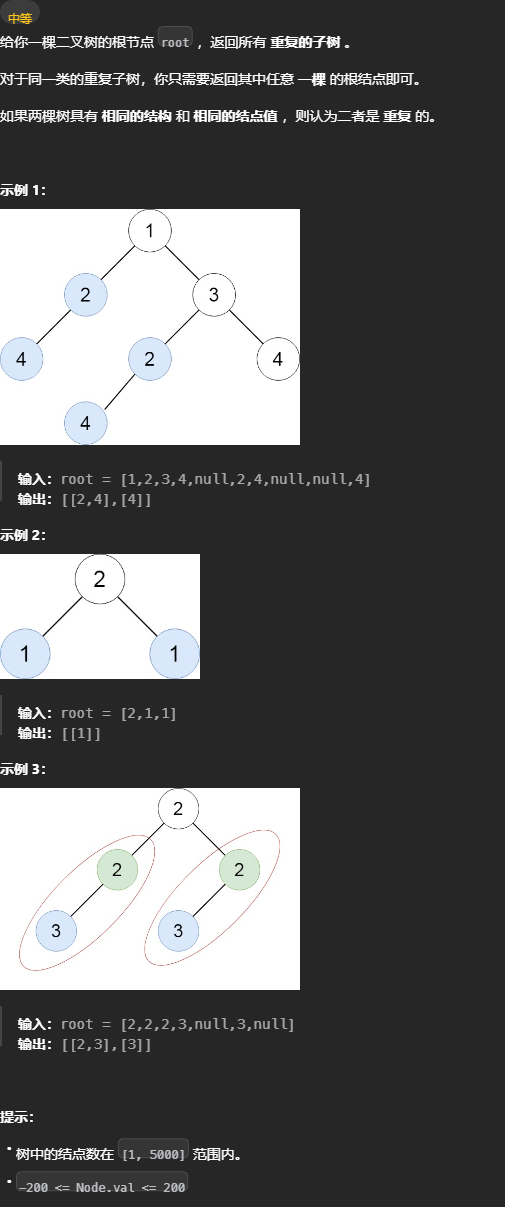
判断节点是否重复
- 需要知道以自己为根的树是怎样的。
- 需要知道其他树是怎样的（需要额外变量维护）。
- 需要两树进行对比。
操作：
- 在后序位置，以自己为根的树递归完成，本树已知。
- 其他树可以在递归前序位置推入。
- 两树对比，用递归。
上面思路没问题，但是两树对比时用递归，时间和空间复杂度都太高了。 树节点可以用它的值代表自身，空节点用 # 替代，这样便可以用文本替代整个树节点。 文本相等对比，时间和空间复杂度大大降低。 由于树用文本序列化表示，要表示一棵树得在后续位置才能知道本树长得怎样。函数返回值为本树序列化。
优化后操作：
- 在后序位置，以自己为根的树递归完成，本树已知
- 其他树可以在递归后序位置维护在
map中 - 两树对比，在
map中找到即重复。 - 因为重复只需要返回一次，所以
map中值用计数器替代布尔值，计数器为2时推入返回数组。
var findDuplicateSubtrees = function(root) {
const map = new Map()
const ret = []
const traverse = root => {
if (!root) return '#'
let left = traverse(root.left)
let right = traverse(root.right)
const treeStr = left + ',' + right + ',' + root.val
const count = (map.get(treeStr) || 0) + 1
map.set(treeStr, count)
if (count === 2) {
ret.push(root)
}
return treeStr
}
traverse(root)
return ret
};
归并排序
框架
对 nums[low..high] 进行排序，归并排序思路：
- 去中点
mid，对nums[low..mid]进行排序，再对nums[mid+1..high]排序 - 最后把这两个有序的子数组合并，整个数组就排好序了 归并排序是一个后序遍历。
// 定义：排序 nums[low..high]
// 重点关注后序遍历位置
function mergeSort(nums, low, high) {
if (low >= high) return
const mid = (low + high) / 2;
// 排序 nums[low..mid]
mergeSort(nums, low, mid);
// 排序 nums[mid+1..hi]
mergeSort(nums, mid + 1, high);
/****** 后序位置 ******/
// 此时两部分子数组已经被排好序
// 合并 nums[low..mid] 和 nums[mid+1..high]
merge(nums, low, mid, high);
/*********************/
}
课本上的总结：归并排序就是先把左半边数组排好序，再把右半边数组排好序，然后把两半数组合并。
上述代码和二叉树的后序遍历很像：
/* 二叉树遍历框架 */
function traverse(root) {
if (root == null) {
return;
}
traverse(root.left);
traverse(root.right);
/****** 后序位置 ******/
console.log(root.val);
/*********************/
}
学会抽象成树
二叉树问题分为两类思路：
- 遍历一遍二叉树
- 分解问题
归并排序利用的是分解问题的思路（分治算法）： 归并排序的过程可以在逻辑上抽象成一棵二叉树，树上的每个节点的值可以认为是 nums[lo..hi]，叶子节点的值就是数组中的单个元素。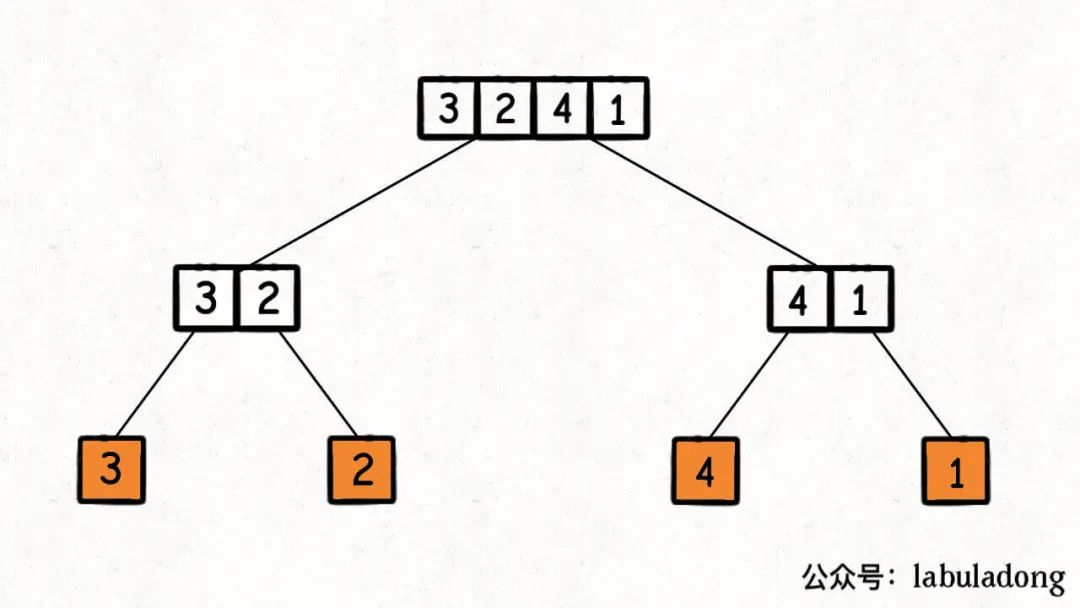
归并操作最后会用 merge 合并，这个 merge 操作会在二叉树的每个节点上都执行一遍，执行顺序是二叉树后序遍历的顺序。即 左 -> 右 -> 根 从左节点树的最底层排序合并，再右节点树，直至根节点，排序完成。顺序如下图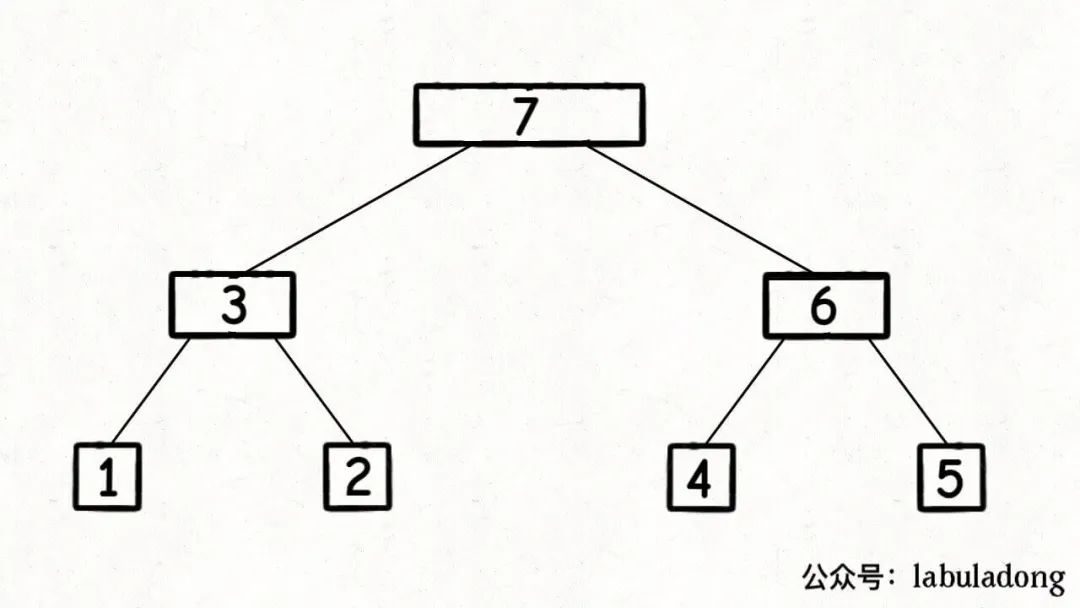 
具体代码实现
class Merge {
constructor(nums) {
this.nums = nums
this.temp = []
this.sort(0, this.nums.length - 1)
}
sort(low, high) {
// 单个元素不用排序
if (low >= high) return
// 效果等同于 (hi + lo) / 2
const mid = low + Math.floor((high - low) / 2)
// 左半部分数组 nums[lo..mid] 排序
this.sort(low, mid)
// 再对右半部分数组 nums[mid+1..hi] 排序
this.sort(mid + 1, high)
// 将两部分有序数组合并成一个有序数组
this.merge(low, mid, high)
}
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
merge(low, mid, high) {
// 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (let i = low; i <= high; i++) {
this.temp[i] = this.nums[i];
}
// 数组双指针技巧，合并两个有序数组
let i = low, j = mid + 1;
for (let p = low; p <= high; p++) {
if (i === mid + 1) {
// 左半边数组已全部被合并
this.nums[p] = this.temp[j++];
} else if (j == high + 1) {
// 右半边数组已全部被合并
this.nums[p] = this.temp[i++];
} else if (this.temp[i] > this.temp[j]) {
this.nums[p] = this.temp[j++];
} else {
this.nums[p] = this.temp[i++];
}
}
}
}
主要看 merge 函数，思路跟拼接两个有序链表类似。分解步骤来看
- 使用两个指针
i和j分别指向左半边数组和右半边数组的起始位置
let i = low, j = mid + 1;
- 使用一个循环，比较
this.temp[i]和this.temp[j]的大小，小的维护到this.nums中，继续移动指针。jsfor (let p = low; p <= high; p++) { if (this.temp[i] > this.temp[j]) { this.nums[p] = this.temp[j++]; } else { this.nums[p] = this.temp[i++]; } } - 如果某一边的数组已经全部被合并，而另一边还有剩余元素，则直接将剩余元素放入原数组
this.nums中jsfor (let p = low; p <= high; p++) { if (i === mid + 1) { // 左半边数组已全部被合并 this.nums[p] = this.temp[j++]; } else if (j == high + 1) { // 右半边数组已全部被合并 this.nums[p] = this.temp[i++]; } } - 汇总js
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组 merge(low, mid, high) { // 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (let i = low; i <= high; i++) {
this.temp[i] = this.nums[i];
}
// 数组双指针技巧，合并两个有序数组
let i = low, j = mid + 1;
for (let p = low; p <= high; p++) {
if (i === mid + 1) {
// 左半边数组已全部被合并
this.nums[p] = this.temp[j++];
} else if (j === high + 1) {
// 右半边数组已全部被合并
this.nums[p] = this.temp[i++];
} else if (this.temp[i] > this.temp[j]) {
this.nums[p] = this.temp[j++];
} else {
this.nums[p] = this.temp[i++];
}
} } ```
归并复杂度为 O(NlogN)，如何计算的？ 计算公式为：子问题个数 x 解决一个子问题的复杂度
merge函数到底执行了多少次？merge函数复杂度是多少？ 但是这种方式很难计算出复杂度，因为每次merge里循环的次数不一致。
换一个思维，在每一层中，循环的次数都是固定的 n，此时有多少层，便是循环了多少次 n，层数为 log₂(n)，所以归并复杂度 O(NlogN)。
- 在每一层，将数组分为两半，每个子数组都需要排序。
- 树的深度是 log₂(n)，因为每次都将数组对半分。
- 在每一层，都需要 O (n)的操作（比较和合并）。
- 因此，总的时间复杂度是 O (n log n)。
merge 方法需要对 nums[lo..mid] 和 nums[mid+1..hi] 两数组合并，由于没法原地合并，需要借助 temp 辅助数组。
temp数组不要在merge函数中声明，因为会在递归中频繁new和释放，有性能问题。
计算右侧小于当前元素的个数
315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）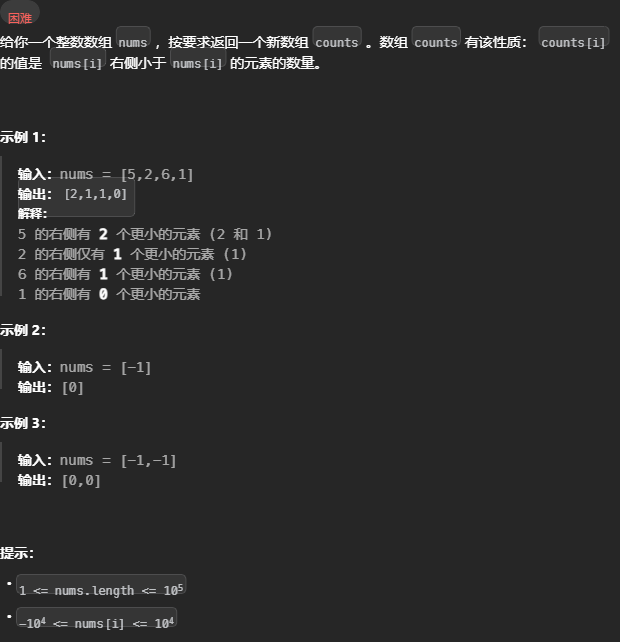
这道题有些技巧性，利用了归并排序相同的解题框架。 归并排序过程中，会对比 temp[i] 和 temp[j] 的大小，取小的作为 nums[p] 值。
// 数组双指针技巧，合并两个有序数组
let i = low, j = mid + 1;
for (let p = low; p <= high; p++) {
if (this.temp[i] > this.temp[j]) {
this.nums[p] = this.temp[j++];
} else {
this.nums[p] = this.temp[i++];
}
}
举个例子，原数组为 [5, 3, 2, 1]，我们把视角落在 5 上，计数右侧比 5 小的数量。 在递归时，是左半边数组先排序，进入左半边数组后再进行分组，此时是 5 和 3 进行对比，由于 3 比 5 小，排序时选用了 3，这就是我们想计数的量，排序时我们进行计数。【比 5 小的计数】
可能会有疑问：temp 数组一直在变，怎么反应原数组右侧小于自身的元素数量？ temp 数组确实一直在变，但只有在两个分组中，右分组比左分组元素小才会被交换过去，对于左分组元素而言（重点，对于左分组元素而言），排序后右分组元素就在前面了，不会被重复计算。例如 [5, 3, 2, 1] 的 3 排序后 [3, 5, 2, 1]，对于 5 而言，3 只会计算一次，3 便一直在 5 前面。
注意：主体是左分组元素
5，因为计数都是对于左分组元素而言的。
对于原数组 [5, 3, 2, 1]，我们视角来到 3。归并序至最后一次数组 [3, 5, 1, 2]，此时我们 i = 0, j = 4 时，这个时候才轮到左分组 3 需要赋值到已排序数组中。次数应该如何计算？[3, 5, 1, 2] 对于 3 而言，应该计数比它小的值为 2 因为有 1、2 两个数字。
原理如下。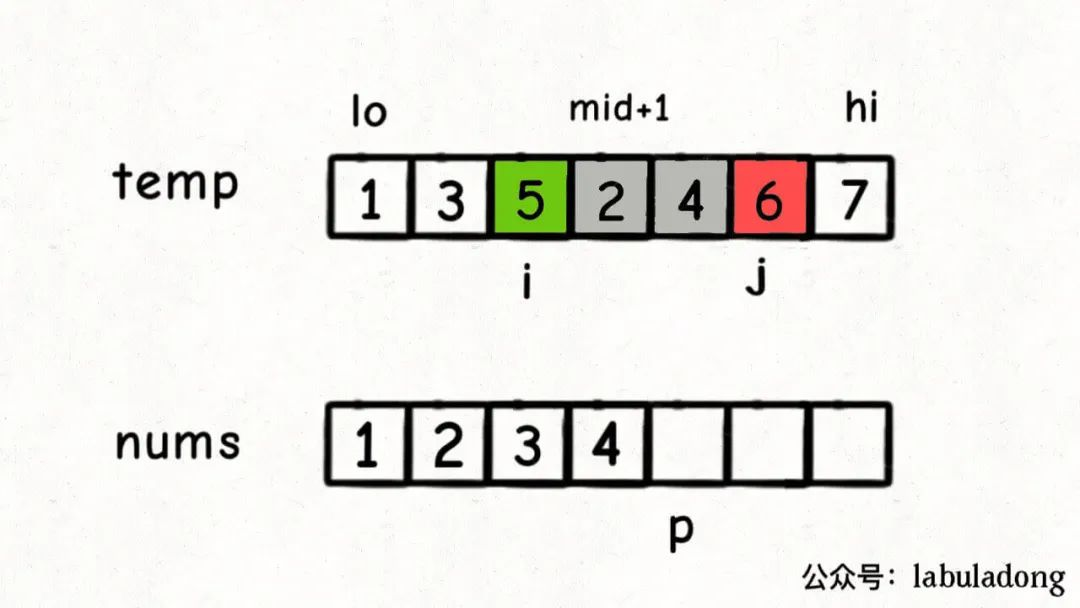 
每一次递归，temp 数组左、右半边数组都是有序递增的，i 和 j 下标对应值小的，对应下标递增。 当 i 被排序时，nums[i] < nums[j]，比 i 小的是 [mid + 1, j - 1]，长度为 j - mid - 1.
所以我们拿归并排序代码框架改一改，可以解答本题。 由于数组的数据不唯一，所以不能用一个对象映射计数。
class Pair {
constructor(num, i) {
this.val = num
this.index = i
}
}
/**
* @param {number[]} nums
* @return {number[]}
*/
var countSmaller = function(nums) {
const temp = []
const arr = []
for (let i = 0; i < nums.length; i++) {
arr.push(new Pair(nums[i], i))
}
const count = new Array(nums.length).fill(0)
const sort = (low, high) => {
// 单个元素不用排序
if (low >= high) return
// 效果等同于 (hi + lo) / 2
const mid = low + Math.floor((high - low) / 2)
// 左半部分数组 nums[lo..mid] 排序
sort(low, mid)
// 再对右半部分数组 nums[mid+1..hi] 排序
sort(mid + 1, high)
// 将两部分有序数组合并成一个有序数组
merge(low, mid, high)
}
const merge = (low, mid, high) => {
// 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (let i = low; i <= high; i++) {
temp[i] = arr[i];
}
// 数组双指针技巧，合并两个有序数组
let i = low, j = mid + 1;
for (let p = low; p <= high; p++) {
if (i === mid + 1) {
// 左半边数组已全部被合并
arr[p] = temp[j++];
} else if (j === high + 1) {
// 右半边数组已全部被合并
arr[p] = temp[i++];
// 重点这一句
count[arr[p].index] += j - mid - 1
} else if (temp[i].val > temp[j].val) {
arr[p] = temp[j++];
} else {
arr[p] = temp[i++];
// 重点这一句
count[arr[p].index] += j - mid - 1
}
}
}
sort(0, arr.length - 1)
return count
};
二叉搜索树 BST
特性
- 对于 BST 的每一个节点
node，左子树节点的值都比node的值要小，右子树节点的值都比node的值大。 - 对于 BST 的每一个节点
node，它的左侧子树和右侧子树都是 BST。 - BST 的中序遍历结果是升序的
拥有了自平衡性质，可以提供 logN 级别的增删查改效率。
BST 的中序遍历结果是升序的
230. 二叉搜索树中第K小的元素 - 力扣（LeetCode）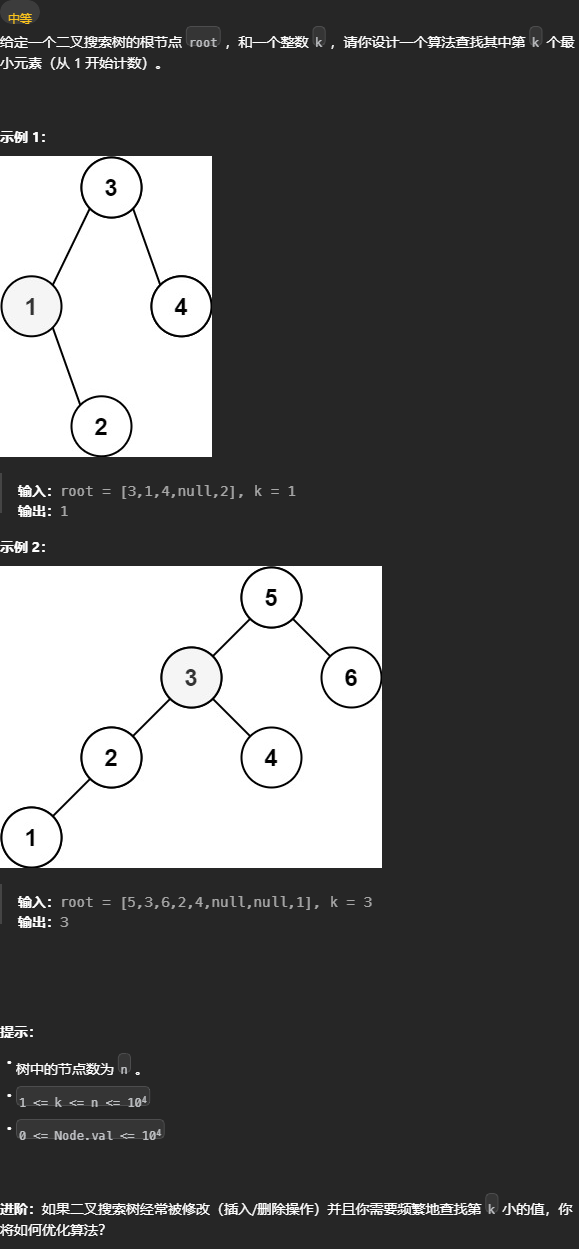
二叉搜索树中序是升序的，所以只要在中序位置取计数，就可以在计数器匹配时返回对应值。 一次遍历可以解决问题，不需要依赖函数返回值。
var kthSmallest = function(root, k) {
let ret
const traverse = (root) => {
root.left && traverse(root.left)
/* 中序位置 */
k--
if (!k) {
ret = root.val
return
}
root.right && traverse(root.right)
}
traverse(root)
return ret
};
这道题的时间复杂度为 O(n)，前面不是说 BST 有自平衡性质，可以提供 logN 级别的增删查改效率吗？ 其实 logN 级别是优化过后的 BST，BST 我们都知道左节点数必定比当前节点小，所以只要知道左节点数量，就知道当前节点排名了，优化后的 BST 需要维护子节点数量。 你可能会疑惑：当前节点的排名，不用关心父节点及祖父有多少节点吗？ 不需要，因为排序只跟数值比当前小的有关， BST 左子树节点的值都比当前节点的值要小。